题目内容
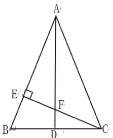
【题目】如图,AD为△ABC的中线,AB=AC,∠BAC=45.过点C 作CE⊥AB,垂足为E,CE与AD交于点F.
(1)求证: △AEF≌△CEB;
(2)试探索AF与CD的数量关系,并说明理由.
【答案】(1) 见解析;(2) ![]() ,理由见解析
,理由见解析
【解析】
(1)根据三线合一可得:![]() ,AD⊥BC,从而得出∠ADB=90°,然后根据等腰直角三角形的判定,可得△AEC为等腰直角三角形,从而得出AE=CE,再根据同角的余角相等可得∠BAD =∠ECB,最后利用ASA即可证出△AEF≌△CEB;
,AD⊥BC,从而得出∠ADB=90°,然后根据等腰直角三角形的判定,可得△AEC为等腰直角三角形,从而得出AE=CE,再根据同角的余角相等可得∠BAD =∠ECB,最后利用ASA即可证出△AEF≌△CEB;
(2)根据全等三角形的性质可得:AF=CB,从而得出![]() .
.
解:(1)∵AD为△ABC的中线,AB=AC,
∴![]() ,AD⊥BC,
,AD⊥BC,
∴∠ADB=90°
∴∠BAD+∠B=90°
∵CE⊥AB,∠BAC=45
∴∠BEC=∠FEA=90°,△AEC为等腰直角三角形
∴∠ECB+∠B=90°,AE=CE
∴∠BAD =∠ECB
在△AEF和△CEB中
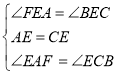
∴△AEF≌△CEB;
(2)![]() ,理由如下:
,理由如下:
∵△AEF≌△CEB
∴AF=CB
∵![]()
∴![]()

练习册系列答案
相关题目