题目内容
【题目】如图1,在矩形![]() 中,
中,![]() 为
为![]() 边上一点
边上一点![]() ,
,![]() .将
.将![]() 沿
沿![]() 翻折得到
翻折得到![]() ,
,![]() 的延长线交边
的延长线交边![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .
.
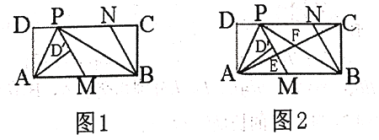
(1)求证:![]() ;
;
(2)如图2,连接![]() 分别交
分别交![]() 、
、![]() 于点
于点![]() 、
、![]() .若
.若![]() ,探究
,探究![]() 与
与![]() 之间的数量关系.
之间的数量关系.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)过点![]() 作
作![]() 于点
于点![]() ,根据矩形的判定可得四边形
,根据矩形的判定可得四边形![]() 和四边形
和四边形![]() 是矩形,从而得出
是矩形,从而得出![]() ,
,![]() ,
,![]() ,然后证出
,然后证出![]() ,列出比例式,再利用等量代换即可得出结论;
,列出比例式,再利用等量代换即可得出结论;
(2)设![]() ,则
,则![]() ,先证出
,先证出![]() ,可得
,可得![]() ,然后证出
,然后证出![]() ,可得
,可得![]() ,即可求出EF和AC的关系,从而求出
,即可求出EF和AC的关系,从而求出![]() 与
与![]() 之间的数量关系.
之间的数量关系.
(1)证明:过点![]() 作
作![]() 于点
于点![]() ,如图1所示:
,如图1所示:
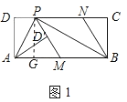
则四边形![]() 和四边形
和四边形![]() 是矩形,
是矩形,
∴![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ;
;
(2)解:∵![]() ,
,
∴设![]() ,则
,则![]() ,
,
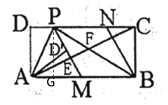
由(1)可知:![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
根据翻折的性质可得![]()
∵DC∥AB,∠APB=90°
∴![]()
![]() +∠BPM=90°,∠PAM+∠PBM=90°
+∠BPM=90°,∠PAM+∠PBM=90°
∴![]() ∠BPM=∠PBM
∠BPM=∠PBM
∴MP=MA,MP=MB
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴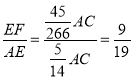 .
.

练习册系列答案
相关题目
【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:
x | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
下列结论:(1)ac<0;
(2)抛物线顶点坐标为(1,5);
(3)3是方程ax2+(b﹣1)x+c=0的一个根;
(4)当﹣1<x<3时,ax2+(b﹣1)x+c>0.其中正确的序号为___________________.