Question

【题目】如图一座拱桥的示意图，已知桥洞的拱形是抛物线.当水面宽为12m时，桥洞顶部离水面4m.、

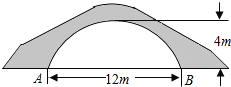
（1）建立平面直角坐标系，并求该抛物线的函数表达式；

（2）若水面上升1m，水面宽度将减少多少？

Answer 1

【答案】(1)图见解析，抛物线的函数表达式为（注：因建立的平面直角坐标系的不同而不同）；(2)

【解析】

（1）以AB的中点为平面直角坐标系的原点O，AB所在线为x轴，过点O作AB的垂线为y轴建立平面直角坐标系（图见解析）；因此，抛物线的顶点坐标为，可设抛物线的函数表达式为，再将B点的坐标代入即可求解；

（2）根据题（1）的结果，令求出x的两个值，从而可得水面上升1m后的水面宽度，再与12m作差即可得出答案.

（1）以AB的中点为平面直角坐标系的原点O，AB所在线为x轴，过点O作AB的垂线为y轴，建立的平面直角坐标系如下：

根据所建立的平面直角坐标系可知，B点的坐标为，抛物线的顶点坐标为

因此设抛物线的函数表达式为

将代入得：

解得：

则所求的抛物线的函数表达式为（注：因建立的平面直角坐标系的不同而不同）；

（2）由题意，令得

解得：

则水面上升1m后的水面宽度为：（米）

故水面上升1m，水面宽度将减少米.