题目内容
在△ABC中,点D是AB边的中点,点E是AC边的中点,连接DE,若BC=4,则DE= .
考点:三角形中位线定理
专题:
分析:根据三角形的中位线平行于第三边并且等于第三边的一半可得DE=
BC.
| 1 |
| 2 |
解答:解:∵点D是AB边的中点,点E是AC边的中点,
∴DE是△ABC的中位线,
∴DE=
BC=
×4=2.
故答案为:2.
∴DE是△ABC的中位线,
∴DE=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:2.
点评:本题考查了三角形的中位线平行于第三边并且等于第三边的一半,熟记定理是解题的关键.

练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
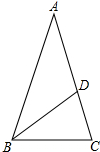 如图,在△ABC中,AB=AC,点D是AC上一点,且AD=BD,若∠C=75°,则∠ADB=( )
如图,在△ABC中,AB=AC,点D是AC上一点,且AD=BD,若∠C=75°,则∠ADB=( )| A、150° | B、120° |
| C、130° | D、110° |
下列运算中,正确的是( )
| A、ab2÷a=b2 |
| B、a2+a3=a5 |
| C、(-2a)3=-6a3 |
| D、3a-a=3 |
 已知:如图,?ABCD中,DE⊥AC于E,BF⊥AC于F.求证:DE=BF.
已知:如图,?ABCD中,DE⊥AC于E,BF⊥AC于F.求证:DE=BF.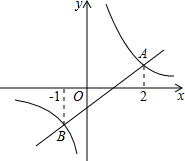 如图,一次函数y1=k1x+b(k1≠0)的图象与反比例函数y2=
如图,一次函数y1=k1x+b(k1≠0)的图象与反比例函数y2= 如图,一只蚂蚁从A沿圆柱表面爬到B处,如果圆柱的高为8cm,圆柱的底面半径为
如图,一只蚂蚁从A沿圆柱表面爬到B处,如果圆柱的高为8cm,圆柱的底面半径为