题目内容
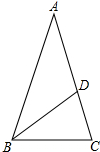如图，在△ABC中，AB=AC，点D是AC上一点，且AD=BD，若∠C=75°，则∠ADB=（ ）| A、150° | B、120° |
| C、130° | D、110° |
考点：等腰三角形的性质
专题：
分析：先根据等腰三角形的性质求出∠ABC的度数，再由三角形内角和定理求出∠A的度数，由BD=AD，可得出∠ABD的度数，在△ABD中根据三角形内角和定理即可得出结论．
解答：解：∵AB=AC，∠C=75°，
∴∠ABC=∠C=75°，
∴∠A=180°-75°-75°=30°，
∵BD=AD，
∴∠A=∠ABD=30°，
∴∠ADB=180°-∠A-∠ABD=120°．
故选B．
∴∠ABC=∠C=75°，
∴∠A=180°-75°-75°=30°，
∵BD=AD，
∴∠A=∠ABD=30°，
∴∠ADB=180°-∠A-∠ABD=120°．
故选B．
点评：本题考查的是等腰三角形的性质，熟知等腰三角形的两底角相等是解答此题的关键．
练习册系列答案
相关题目
下列整式中与3a2b2c3是同类项的有（ ）
| A、5c3a2b2 | ||
| B、-3a2b2c2 | ||
C、
| ||
| D、3a2bc3 |
为了了解一片实验田的某种水稻的穗长情况，从中抽取了400个稻穗测量长度，结果有40个稻穗测量长度超过超过30cm，在这个问题中，下列说法正确的是（ ）
| A、400个稻穗的穗长情况是总体 |
| B、40个稻穗的穗长情况是样本 |
| C、每个稻穗的穗长情况是个体 |
| D、样本容量是40 |
如图，直线a∥b，∠1=115°，∠2=105°，则∠3的度数为（ ）| A、120° | B、130° |
| C、140° | D、80° |
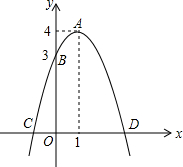如图，已知抛物线的顶点为A（1，4），抛物线与y轴交于点B（0，3），与x轴交于C、D两点，点P是x轴上的一个动点．