题目内容
 如图,点P在圆O外,PA与圆O相切于A点,OP与圆周相交于C点,已知OA=1,PA=
如图,点P在圆O外,PA与圆O相切于A点,OP与圆周相交于C点,已知OA=1,PA= .则S阴影=________.
.则S阴影=________.
 -
-
分析:先根据切线的性质得到OA⊥PA,即∠PAO=90°,再根据正切的定义计算出∠AOP=60°,然后根据三角形的面积公式和扇形的面积公式,利用S阴影=S△OAP-S扇形OAC进行计算即可.
解答:∵PA与圆O相切于A点,
∴OA⊥PA,
∴∠PAO=90°,
∵OA=1,PA=
 ,
,∴tan∠AOP=
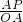 =
= ,
,∴∠AOP=60°,
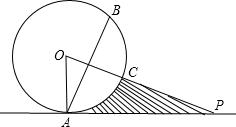
∴S阴影=S△OAP-S扇形OAC=
 ×1×
×1× -
-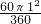 =
= -
- .
.故答案为
 -
- .
.点评:本题切线的性质:圆的切线垂直于经过切点的半径;经过圆心且垂直于切线的直线必经过切点;经过切点且垂直于切线的直线必经过圆心.也考查了扇形的面积公式.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
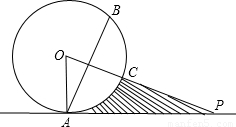
 直线PO对称,已知OA=4,PA=
直线PO对称,已知OA=4,PA=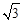 .
.
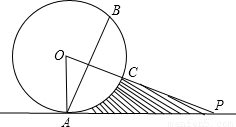 直线PO对称,已知OA=4,PA=
直线PO对称,已知OA=4,PA=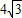 .求:
.求: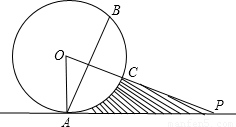 直线PO对称,已知OA=4,PA=
直线PO对称,已知OA=4,PA=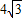 .求:
.求: