题目内容
如图,点P在圆O外,PA与圆O相切于A点,OP与圆周相交于C点,点B与点A关于直线PO对称,已知OA=4,PA=4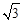 .
.
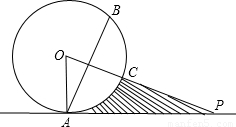
求:(1)∠POA的度数;
(2)弦AB的长;
(3)阴影部分的面积(结果保留π).
【答案】
(1)60°;(2)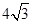 ;(3)
;(3) .
.
【解析】
试题分析:(1)由切线的性质得直角三角形OAP,应用正切函数即可求得∠POA的度数;(2)根据对称的性质,应用垂径定理和余弦函数即可求得弦AB的长;(3)根据转换思想疳阴影面积转化为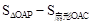 求解即可.
求解即可.
试题解析:(1)∵PA切圆与A,∴OA⊥PA.
又∵OA=4,PA=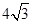 ,
∴
,
∴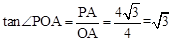 . ∴∠POA = 60°.
. ∴∠POA = 60°.
(2)设AB与OP的交点为D,
∵点B与点A关于直线PO对称,∴AD=BD.
∵OC为半径,AD=BD,∴OC⊥AB. ∴∠OAD=90°-∠AOD=30°.
∴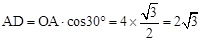 。∴AB=2AD=
。∴AB=2AD=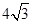 .
.
(3)∵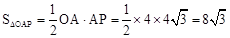 ,
,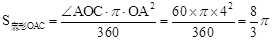 ,
,
∴阴影面积= .
.
考点:1.切线的性质;2.锐角三角函数定义;3.特殊角的三角函数值;4.对称的性质;5.垂径定理;6.扇形面积;7.转换思想的应用.

练习册系列答案
相关题目
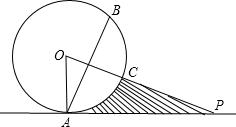 直线PO对称,已知OA=4,PA=
直线PO对称,已知OA=4,PA= 直线PO对称,已知OA=4,PA=
直线PO对称,已知OA=4,PA=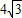 .求:
.求: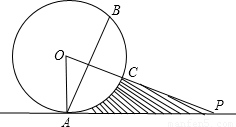 直线PO对称,已知OA=4,PA=
直线PO对称,已知OA=4,PA=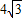 .求:
.求: