题目内容
如图,点P在圆O外,PA与圆O相切于A点,OP与圆周相交于C点,点B与点A关于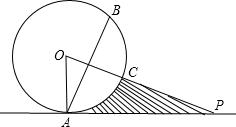 直线PO对称,已知OA=4,PA=4
直线PO对称,已知OA=4,PA=4| 3 |
(1)∠POA的度数;
(2)弦AB的长;
(3)阴影部分的面积.
分析:(1)根据AP是圆的切线,则得到△OAP是直角三角形,根据OA,PA的值,就可以∠POA的度数;
(2)AB⊥PO,设AB与PO相交于点D,则AB=2AD,在直角△OAD中,根据三角函数就可以求出AD的长,从而求出AB的长;
(3)设阴影部分面积为s,则S=S△OAP-S扇形AOC,分别求出△OAP与扇形AOC的面积就可以求出.
(2)AB⊥PO,设AB与PO相交于点D,则AB=2AD,在直角△OAD中,根据三角函数就可以求出AD的长,从而求出AB的长;
(3)设阴影部分面积为s,则S=S△OAP-S扇形AOC,分别求出△OAP与扇形AOC的面积就可以求出.
解答: 解:(1)∵PA是圆O的切线,切点是A.
解:(1)∵PA是圆O的切线,切点是A.
∴OA⊥PA.
在Rt△APO中,tan∠POA=
=
,
∴∠POA=60°;3分
(2)设AB与PO相交于点D,如图,
∵点B与点A关于直线PO对称,
∴AB⊥PO,且AB=2AD,
在Rt△ADO中,AD=OAsin60°=2
,
∴AB=2AD=4
;4分
(3)设阴影部分面积为s,
则S=S△OAP-S扇形AOC,
∵S△OAP=8
,S扇形AOC=
,
∴S=8(
-
).3分
 解:(1)∵PA是圆O的切线,切点是A.
解:(1)∵PA是圆O的切线,切点是A.∴OA⊥PA.
在Rt△APO中,tan∠POA=
| PA |
| OA |
| 3 |
∴∠POA=60°;3分
(2)设AB与PO相交于点D,如图,
∵点B与点A关于直线PO对称,
∴AB⊥PO,且AB=2AD,
在Rt△ADO中,AD=OAsin60°=2
| 3 |
∴AB=2AD=4
| 3 |
(3)设阴影部分面积为s,
则S=S△OAP-S扇形AOC,
∵S△OAP=8
| 3 |
| 8π |
| 3 |
∴S=8(
| 3 |
| π |
| 3 |
点评:本题主要考查了垂径定理,三角函数,求阴影部分的面积可以转化为一些规则图形的面积的和或差来计算.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案
相关题目
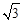 .
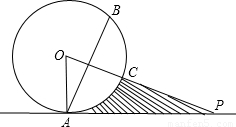
.
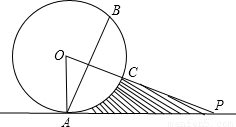 直线PO对称,已知OA=4,PA=
直线PO对称,已知OA=4,PA=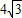 .求:
.求: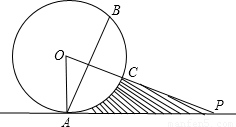 直线PO对称,已知OA=4,PA=
直线PO对称,已知OA=4,PA=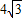 .求:
.求: