Question

12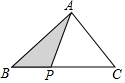．如图，已知△ABC中，点P从点B出发，沿BC向终点C运动，当到达点C时停止运动，设PB=x，则△PAB（图中阴影部分）的面积S与x之间的关系用图可以表示为（　　）

• A．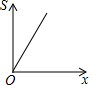
• B．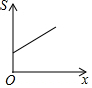
• C．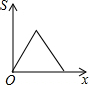
• D．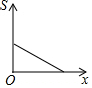

Answer 1

分析 作△ABC的高AD，则AD为定值．根据三角形的面积公式得出S=$\frac{1}{2}$PB•AD=$\frac{1}{2}$x•AD=$\frac{1}{2}$AD•x，判断得到S是x的正比例函数，根据正比例函数的图象与性质即可求解．

解答 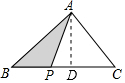解：如图，作△ABC的高AD，则AD为定值．
△PAB（图中阴影部分）的面积S=$\frac{1}{2}$PB•AD=$\frac{1}{2}$x•AD=$\frac{1}{2}$AD•x，
即S=$\frac{1}{2}$AD•x，
∵AD为定值，
∴$\frac{1}{2}$AD为定值，
∴S是x的正比例函数．
故选A．

点评 本题考查了动点问题的函数图象，三角形的面积，正比例函数的定义、图象与性质，求出S与x的函数关系式是解题的关键．