题目内容
如图，左边的楼高AB=60m，右边的楼高CD=24m，且BC=30m，地面上的目标P位于距C点15m处．（1）请画出从A处看地面上距点C最近的点，这个点与点C之间的距离是多少？
（2）从A处能看见目标P吗，为什么？
考点：视点、视角和盲区
专题：
分析：（1）连接AD并延长，与地面相交于点E，交点E即为所求的点，再利用相似三角形对应边成比例列式求解即可；
（2）根据EC和PC的距离判断即可．
（2）根据EC和PC的距离判断即可．
解答：
解：（1）如图，连接AD并延长，与地面相交于点E，
则点E即为从A处看地面上距点C最近的点，
∵AB、CD都与地面垂直，
∴AB∥CD，
∴△ABE∽△DCE，
∴
=
，
即
=
，
解得CE=20，
答：这个点与点C之间的距离是20米；
（2）∵目标P位于距C点15m处，
∴CE＞PC，
∴从A处不能看见目标P．
解：（1）如图，连接AD并延长，与地面相交于点E，则点E即为从A处看地面上距点C最近的点，
∵AB、CD都与地面垂直，
∴AB∥CD，
∴△ABE∽△DCE，
∴
| AB |
| CD |
| BE |
| CE |
即
| 60 |
| 24 |
| 30+CE |
| CE |
解得CE=20，
答：这个点与点C之间的距离是20米；
（2）∵目标P位于距C点15m处，
∴CE＞PC，
∴从A处不能看见目标P．
点评：本题考查相似三角形的判定与性质的实际应用及分析问题、解决问题的能力．利用数学知识解决实际问题是中学数学的重要内容．解决此问题的关键在于正确理解题意的基础上建立数学模型，把实际问题转化为数学问题．
练习册系列答案
单元全能练考卷系列答案
新黄冈兵法密卷系列答案
相关题目
如图，把一个边长为a的正三角形纸片剪成正六边形，减去的三个小三角形的边长应是多少？
如图，直线y=
把一张长方形纸片（ABCD）沿GH折叠，使点B与点D重合，BD=10cm，∠DGH=55°，求∠DHC的角度．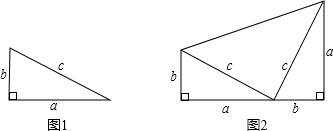
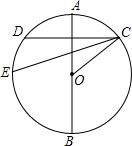如图，小明从小就喜欢动手动脑，请看他的研究：（1）以AB为直径画⊙O；（2）在⊙O上取一点C，过点C作弦CD⊥AB；（3）画∠OCD的平分线交⊙O于点E；如图他发现：①AB平分CD；②AB平分
用8个直角三角形纸片拼出如图所示的形状，图中的3个正方形的面积之间有何关系？请用a，b，c将此关系表示出来．
已知：如图∠1=∠2，∠3=∠4，求证：△ABC≌△ABD．