题目内容
13.现有50张大小、质地及背面图案均相同的《西游记》任务卡片,正面朝下放置在桌面上,从中随机抽取一张并记下卡片正面所绘人物的名字后原样放回,洗匀后再抽.通过多次试验后,发现抽到绘有孙悟空这个人物卡片的频率约为0.2.估计这些卡片中绘有孙悟空这个人物的卡片张数约为10.分析 利用频率估计概率得到抽到绘有孙悟空这个人物卡片的概率为0.3,则根据概率公式可计算出这些卡片中绘有孙悟空这个人物的卡片张数,于是可估计出这些卡片中绘有孙悟空这个人物的卡片张数.
解答 解:因为通过多次试验后,发现抽到绘有孙悟空这个人物卡片的频率约为0.3,
所以估计抽到绘有孙悟空这个人物卡片的概率为0.2,
则这些卡片中绘有孙悟空这个人物的卡片张数=0.2×50=10(张).
所以估计这些卡片中绘有孙悟空这个人物的卡片张数约为10张.
故答案为:10;
点评 本题考查了频率估计概率:用频率估计概率得到的是近似值,随实验次数的增多,值越来越精确.

练习册系列答案
相关题目
1. 如图,阴影部分是一个长方形,它的面积是( )
如图,阴影部分是一个长方形,它的面积是( )
 如图,阴影部分是一个长方形,它的面积是( )
如图,阴影部分是一个长方形,它的面积是( )| A. | 3cm2 | B. | 4cm2 | C. | 5cm2 | D. | 6cm2 |
5.下列分式中,是最简分式的是( )
| A. | $\frac{{a}^{2}+{b}^{2}}{a+b}$ | B. | $\frac{{a}^{2}-{b}^{2}}{a+b}$ | C. | $\frac{a-b}{{a}^{2}-2ab+{b}^{2}}$ | D. | $\frac{6x}{8y}$ |
 如图中几何体由一些完全相同的小立方体组成,从上面看到图形的形状是( )
如图中几何体由一些完全相同的小立方体组成,从上面看到图形的形状是( )




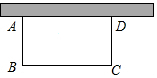 如图,用一段长为40m的篱笆围成一个一边靠墙的矩形花圃ABCD,墙长28m.设AB长为x m,矩形的面积为y m2.
如图,用一段长为40m的篱笆围成一个一边靠墙的矩形花圃ABCD,墙长28m.设AB长为x m,矩形的面积为y m2.