题目内容
9.在进行二次根式简化时,我们有时会碰上如$\frac{5}{\sqrt{3}}$,$\sqrt{\frac{2}{3}}$,$\frac{2}{\sqrt{3}+1}$一样的式子,其实我们还可将其进一步简化:$\frac{3}{\sqrt{5}}=\frac{3×\sqrt{5}}{\sqrt{5}×\sqrt{5}}$=$\frac{3}{5}\sqrt{5}$;(一)
$\sqrt{\frac{2}{3}}$=$\sqrt{\frac{2×3}{3×3}}$=$\frac{\sqrt{6}}{3}$;(二)
$\frac{2}{\sqrt{3}+1}$=$\frac{2(\sqrt{3}-1)}{(\sqrt{3}+1)(\sqrt{3}-1)}$=$\frac{2(\sqrt{3}-1)}{(\sqrt{3})^{2}-{1}^{2}}$=$\sqrt{3}-1$;(三)
以上这种化简的步骤叫做分母有理化
$\frac{2}{\sqrt{3}+1}$还可以用以下方法化简:
$\frac{2}{\sqrt{3}+1}$=$\frac{3-1}{\sqrt{3}+1}$=$\frac{(\sqrt{3})^{2}-{1}^{2}}{\sqrt{3}+1}$=$\frac{(\sqrt{3}+1)(\sqrt{3}-1)}{\sqrt{3}+1}$$\sqrt{3}-1$;(四)
(1)化简$\frac{3}{\sqrt{3}}$=$\sqrt{3}$ $\sqrt{\frac{1}{5}}$=$\frac{\sqrt{5}}{5}$
(2)请用不同的方法化简$\frac{2}{\sqrt{5}+\sqrt{3}}$.
①参照(三)式得$\frac{2}{\sqrt{5}+\sqrt{3}}$=$\sqrt{5}$-$\sqrt{3}$
②步骤(四)式得$\frac{2}{\sqrt{5}+\sqrt{3}}$=$\sqrt{5}$-$\sqrt{3}$
(3)化简:
$\frac{1}{\sqrt{3}+1}$+$\frac{1}{\sqrt{5}+\sqrt{3}}$+$\frac{1}{\sqrt{7}+\sqrt{5}}$+…+$\frac{1}{\sqrt{2n+1}+\sqrt{2n-1}}$.
分析 (1)根据题中所给出的例子把分母化为完全平方式的形式即可;
(2)①根据步骤(三)把分母乘以$\sqrt{5}$-$\sqrt{3}$即可;
②根据步骤(四)把分子化为($\sqrt{5}$-$\sqrt{3}$)($\sqrt{5}$+$\sqrt{3}$)的形式即可;
(3)把各式的分母有理化,找出规律即可得出结论.
解答 解:(1)$\frac{3}{\sqrt{3}}$=$\frac{3\sqrt{3}}{\sqrt{3}•\sqrt{3}}$=$\sqrt{3}$,$\sqrt{\frac{1}{5}}$=$\sqrt{\frac{5}{5×5}}$=$\frac{\sqrt{5}}{5}$.
故答案为:$\sqrt{3}$,$\frac{\sqrt{5}}{5}$;
(2)①原式=$\frac{2(\sqrt{5}-\sqrt{3})}{(\sqrt{5}+\sqrt{3})(\sqrt{5}-\sqrt{3})}$=$\sqrt{5}$-$\sqrt{3}$.
故答案为:$\sqrt{5}$-$\sqrt{3}$;
②原式=$\frac{5-3}{\sqrt{5}+\sqrt{3}}$=$\frac{(\sqrt{5}+\sqrt{3})(\sqrt{5}-\sqrt{3})}{\sqrt{5}+\sqrt{3}}$=$\sqrt{5}$-$\sqrt{3}$.
故答案为:$\sqrt{5}$-$\sqrt{3}$;
(3)原式=$\frac{\sqrt{3}-1}{2}$+$\frac{\sqrt{5}-\sqrt{3}}{2}$+$\frac{\sqrt{7}-\sqrt{5}}{2}$+…+$\frac{\sqrt{2n+1}-\sqrt{2n-1}}{2}$
=$\frac{\sqrt{3}-1+\sqrt{5}-\sqrt{3}+\sqrt{7}-\sqrt{5}+…+\sqrt{2n+1}-\sqrt{2n-1}}{2}$
=$\frac{\sqrt{2n+1}-1}{2}$.
点评 本题考查的是分母有理化,根据题意得出分母有理化的规律是解答此题的关键.

| 甲 | 98 | 100 | 100 | 90 | 96 | 91 | 89 | 99 | 100 | 100 | 93 |
| 乙 | 98 | 99 | 96 | 94 | 95 | 92 | 92 | 98 | 96 | 99 | 97 |
(2)分析他们的成绩各有什么特点;
(3)现要从两人中选一人参加比赛,历届比赛成绩表明,平均成绩达98分以上(含98分)才可能迸人决赛,你认为应该选谁参加这次比赛呢?为什么?
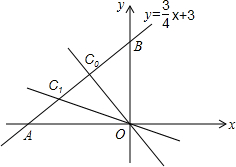 一次函数y=$\frac{3}{4}$x+m的图象过点(4,6),且分别与x轴、y轴交于A、B点,点P(a,0)在x轴正半轴上运动,点Q(0,b)在y轴正半轴上运动.
一次函数y=$\frac{3}{4}$x+m的图象过点(4,6),且分别与x轴、y轴交于A、B点,点P(a,0)在x轴正半轴上运动,点Q(0,b)在y轴正半轴上运动.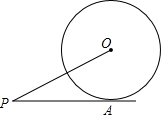 如图,已知PA切⊙O于点A,OP=5,PA比⊙O的半径大1,求⊙O的半径.
如图,已知PA切⊙O于点A,OP=5,PA比⊙O的半径大1,求⊙O的半径.