题目内容
12.判断方程y2-5y-1=0的根的情况( )| A. | 有两个相等的实根 | B. | 有两个不相等的实根 | ||
| C. | 没有实根 | D. | 无法确定 |
分析 根据方程的系数结合根的判别式即可得出△=29>0,由此即可得出结论.
解答 解:∵在方程y2-5y-1=0中,△=(-5)2-4×1×(-1)=29>0,
∴方程y2-5y-1=0有两个不相等的实数根.
故选B.
点评 本题考查了根的判别式,熟练掌握“当△>0时,方程有两个不相等的两个实数根”.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
2.某餐厅共有10名员工,所有员工的工资情况如下表:
则该餐厅所有员工工资的众数、中位数分别是( )
| 人员 | 经理 | 厨师 | 会计 | 保安 | 服务员 |
| 人数(人) | 1 | 2 | 1 | 1 | 5 |
| 工资(元) | 5000 | 4000 | 3500 | 3000 | 2000 |
| A. | 5000,3500 | B. | 5000,2500 | C. | 2000,3500 | D. | 2000,2500 |
7.方程(y+1)(y-1)=2y2-4y-6化为一般形式为( )
| A. | y2-4y+5=0 | B. | y2-4y-5=0 | C. | y2+4y-5=0 | D. | y2+4y+5=0 |
4.如图,有5张扑克牌,从中随机抽取一张牌,点数是偶数的可能性大小是( )


| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
1.下列计算正确的是( )
| A. | ${({-\sqrt{2}})^2}$=2 | B. | $\sqrt{{{({-5})}^2}}$=-5 | C. | $\sqrt{2}÷\sqrt{6}=\sqrt{3}$ | D. | $\sqrt{{a^2}b}=a\sqrt{b}({a<0})$ |
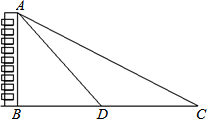 如图,为了测量某建筑物AB高度,在平地上C处测得建筑物顶端A的仰角为30°,沿CB方向前进12m到达D处,在D处测得建筑物顶端A的仰角为45°,则建筑物AB高度等于(6$\sqrt{3}$+6)m.
如图,为了测量某建筑物AB高度,在平地上C处测得建筑物顶端A的仰角为30°,沿CB方向前进12m到达D处,在D处测得建筑物顶端A的仰角为45°,则建筑物AB高度等于(6$\sqrt{3}$+6)m.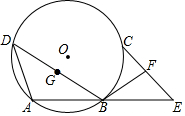 如图,点A、B、C、D在⊙O上,且$\widehat{AD}$=$\widehat{BC}$,E是AB延长线上一点,且BE=AB,F是EC的中点.
如图,点A、B、C、D在⊙O上,且$\widehat{AD}$=$\widehat{BC}$,E是AB延长线上一点,且BE=AB,F是EC的中点.