Question

如图，在平面直角坐标中，直线l经过原点，且与y轴正半轴所夹的锐角为60°，过点A（0，1）作y轴的垂线l于点B，过点B₁作直线l的垂线交y轴于点A₁，以A₁B．BA为邻边作?ABA₁C₁；过点A₁作y轴的垂线交直线l于点B₁，过点B₁作直线l的垂线交y轴于点A₂，以A₂B₁．B₁A₁为邻边作?A₁B₁A₂C₂；…；按此作法继续下去，则C₄的坐标是

 

．

Answer 1

考点：平行四边形的性质,一次函数图象上点的坐标特征

专题：规律型

分析：先求出直线l的解析式为y=

3

3

x，设B点坐标为（x，1），根据直线l经过点B，求出B点坐标为（

3

，1），解Rt△A₁AB，得出AA₁=3，OA₁=4，由平行四边形的性质得出A₁C₁=AB=

3

，则C₁点的坐标为（-

3

，4），即（-

3

×4⁰，4¹）；根据直线l经过点B₁，求出B₁点坐标为（4

3

，4），解Rt△A₂A₁B₁，得出A₁A₂=12，OA₂=16，由平行四边形的性质得出A₂C₂=A₁B₁=4

3

，则C₂点的坐标为（-4

3

，16），即（-

3

×4¹，4²）；同理，可得C₃点的坐标为（-16

3

，64），即（-

3

×4²，4³）；进而得出规律，求得C_n的坐标是（-

3

×4^n-1，4ⁿ），即可得出C₄的坐标．

解答：解：∵直线l经过原点，且与y轴正半轴所夹的锐角为60°，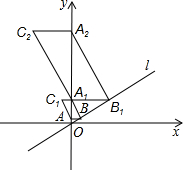
∴直线l的解析式为y=

3

3

x．
∵AB⊥y轴，点A（0，1），
∴可设B点坐标为（x，1），
将B（x，1）代入y=

3

3

x，
得1=

3

3

x，解得x=

3

，
∴B点坐标为（

3

，1），AB=

3

．
在Rt△A₁AB中，∠AA₁B=90°-60°=30°，∠A₁AB=90°，
∴AA₁=

3

AB=3，OA₁=OA+AA₁=1+3=4，
∵?ABA₁C₁中，A₁C₁=AB=

3

，
∴C₁点的坐标为（-

3

，4），即（-

3

×4⁰，4¹）；
由

3

3

x=4，解得x=4

3

，
∴B₁点坐标为（4

3

，4），A₁B₁=4

3

．
在Rt△A₂A₁B₁中，∠A₁A₂B₁=30°，∠A₂A₁B₁=90°，
∴A₁A₂=

3

A₁B₁=12，OA₂=OA₁+A₁A₂=4+12=16，
∵?A₁B₁A₂C₂中，A₂C₂=A₁B₁=4

3

，
∴C₂点的坐标为（-4

3

，16），即（-

3

×4¹，4²）；
同理，可得C₃点的坐标为（-16

3

，64），即（-

3

×4²，4³）；
以此类推，则C_n的坐标是（-

3

×4^n-1，4ⁿ），
故C₄的坐标是：（-

3

×4³，4⁴）即（-64

3

，256），
故答案为：（-64

3

，256）．

点评：本题考查了平行四边形的性质，解直角三角形以及一次函数的综合应用，先分别求出C₁、C₂、C₃点的坐标，从而发现规律是解题的关键．