题目内容
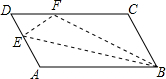 如图,平行四边形ABCD中,点E在边AD上,以BE为折痕,将△ABE折叠,使点A正好与CD上的F点重合.若△FDE的周长为14,△FCB的周长为26,则FC的长为
如图,平行四边形ABCD中,点E在边AD上,以BE为折痕,将△ABE折叠,使点A正好与CD上的F点重合.若△FDE的周长为14,△FCB的周长为26,则FC的长为考点:翻折变换(折叠问题),平行四边形的性质
专题:
分析:先根据折叠的性质得BF=BA,AE=EF,而DE+DF+EF=14,CF+BC+BF=26,则DE+DF+AE=14,即DF+AD=14,CF+BC+AB=26,再根据平行四边形的性质得AD=BC,AB=DC=CF+DF,所以CF+AD+CF+DF=26,即DF+AD+2CF=26,再把DF+AD=14代入得到16+2CF=26,然后解关于CF的方程即可.
解答:解:∵以BE为折痕,将△ABE折叠,使点A正好与CD上的F点重合,
∴BF=BA,AE=EF,
∵△FDE的周长为14,△FCB的周长为26,
∴DE+DF+EF=14,CF+BC+BF=26,
∴DE+DF+AE=14,CF+BC+AB=26,
∴DF+AD=14,
∵四边形ABCD为平行四边形,
∴AD=BC,AB=DC=CF+DF,
∴CF+AD+CF+DF=26,即DF+AD+2CF=26,
∴14+2CF=26,
∴CF=6.
故答案为:6
∴BF=BA,AE=EF,
∵△FDE的周长为14,△FCB的周长为26,
∴DE+DF+EF=14,CF+BC+BF=26,
∴DE+DF+AE=14,CF+BC+AB=26,
∴DF+AD=14,
∵四边形ABCD为平行四边形,
∴AD=BC,AB=DC=CF+DF,
∴CF+AD+CF+DF=26,即DF+AD+2CF=26,
∴14+2CF=26,
∴CF=6.
故答案为:6
点评:本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了平行四边形的性质.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
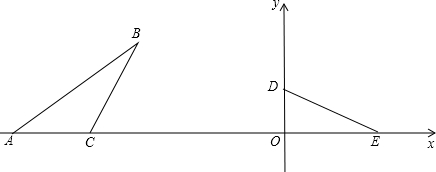
 如图所示,在长方形ABCD中,AB=8cm,BC=6cm,且△BEC的面积比△DEF的面积大5cm2,求DF的长.
如图所示,在长方形ABCD中,AB=8cm,BC=6cm,且△BEC的面积比△DEF的面积大5cm2,求DF的长.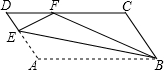 如图,在?ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,点A正好落在CD上的点F处,若△FDE的周长为8,△FCB的周长为32,则FC的长为
如图,在?ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,点A正好落在CD上的点F处,若△FDE的周长为8,△FCB的周长为32,则FC的长为 如图,在矩形ABCD中,AB<BC,AC,BD相交于点O,则图中等腰三角形的个数是
如图,在矩形ABCD中,AB<BC,AC,BD相交于点O,则图中等腰三角形的个数是