题目内容
15. 如图,在△ABC中,AD平分∠BAC,DE∥AC,DF∥AB,求证:AD⊥EF.
如图,在△ABC中,AD平分∠BAC,DE∥AC,DF∥AB,求证:AD⊥EF.
分析 首先利用平行四边形的判定方法可知四边形AEDF是平行四边形,并由DE∥AC利用平行线的性质得到∠DAF=∠ADE,进而得到∠EAD=∠ADE,然后利用等腰三角形的判定可得EA=ED,可知四边形AEDF是菱形,再根据菱形的对角线互相垂直的性质可得结论.
解答 证明:∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,
∵DE∥AC,
∴∠DAF=∠ADE,
又∵AD平分∠BAC,即∠EAD=∠DAF,
∴∠EAD=∠ADE,
∴EA=ED,
∴平行四边形AEDF是菱形,
∴AD⊥EF.
点评 本题考查了菱形的判定与性质,平行四边形的判定,平行线的性质,等腰三角形的判定等知识,正确识图并通过推理得出四边形AEDF是菱形是解题的关键.

练习册系列答案
相关题目
3.下列计算正确的是( )
| A. | (-$\frac{5}{4}$x2)(-4ax)2=5a2x4 | B. | x(2x2-x+1)=2x3-x2+1 | ||
| C. | (a+2b)2=a2+2ab+4b2 | D. | (-3m-2n)(-2n+3m)=4n2-9m2 |
 如图所示,∠1=70°,∠2=70°,∠4=60°,则∠3=120度.
如图所示,∠1=70°,∠2=70°,∠4=60°,则∠3=120度.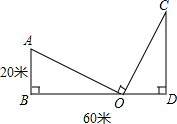 一位同学和妈妈一起逛街时发现了这样一个问题:如图,两座相距60米的大楼,分别从各自楼顶悬挂一条一样的条幅到地面,两条幅拉直后长度相同且他用手里的书测量了一下发现两个条幅互相垂直,最后都固定在地面上同一处,现在这位同学知道其中一座楼高20米,他想了想告诉妈妈他可以在地面上测量出另一座楼的高度,你知道他是怎么做的吗?
一位同学和妈妈一起逛街时发现了这样一个问题:如图,两座相距60米的大楼,分别从各自楼顶悬挂一条一样的条幅到地面,两条幅拉直后长度相同且他用手里的书测量了一下发现两个条幅互相垂直,最后都固定在地面上同一处,现在这位同学知道其中一座楼高20米,他想了想告诉妈妈他可以在地面上测量出另一座楼的高度,你知道他是怎么做的吗? 已知:如图所示,AD是△ABC的高,E为AD上一点,且BE=EC,求证:△ABC是等腰三角形.
已知:如图所示,AD是△ABC的高,E为AD上一点,且BE=EC,求证:△ABC是等腰三角形. 如图,∠1=88°,∠2=88°,∠3=50°,求∠4.
如图,∠1=88°,∠2=88°,∠3=50°,求∠4.