Question

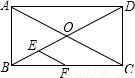
如图，⊙O过正方形ABCD的顶点A、B，且与CD相切，若正方形ABCD的边长为2，则⊙O的半径为（ ）

A．1 B． C． D．

Answer 1

D．

【解析】

试题分析：连接OE、OB，延长EO交AB于F；

∴E是切点，

∴OE⊥CD，

∴OF⊥AB，OE=OB；

设OB=R，则OF=2-R，

在Rt△OBF中，BF=AB=×2=1，OB=R，OF=2-R，

∴R2=（2-R）2+12，

解得R=．

故选：D．

考点：1．切线的性质；2．勾股定理；3．垂径定理．