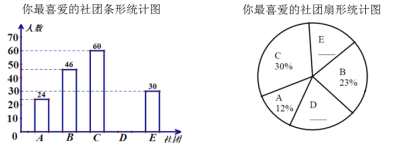
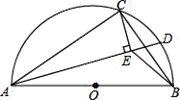
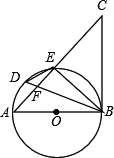
题目内容
【题目】如图,![]() 是
是![]() 的直径,点
的直径,点![]() 是弧
是弧![]() 上一点,且
上一点,且![]() ,
,![]() 与
与![]() 交与点
交与点![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() 平分
平分![]() ,求证:
,求证:![]() ;
;
(3)在(2)的条件下,延长![]() ,
,![]() 交于点
交于点![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长和
的长和![]() 的半径.
的半径.
【答案】(1)证明见解析;(2)证明见解析;(3)![]()
【解析】
(1)已知![]() ,
,![]() ,得到
,得到![]() 根据
根据![]() 是
是![]() 的直径,得到
的直径,得到![]() ,所以
,所以![]() ,即可证明
,即可证明![]() 是
是![]() 的切线.
的切线.
(2)利用同弧所对的圆周角相等和角平分线的定义可得到∠DEA=∠DBE,通过证得△DEF∽△DBE即可求解;
(3)根据题意画出图形,连接DA、DO,不难得到OD∥BE,进而有![]() ,由PA=AO可得到
,由PA=AO可得到![]() ,结合ED的长即可得到PD的长;由圆内接四边形的对角互补可得到∠ABE+∠ADE=180°,结合平角和平行线的性质可得到∠PDA=∠AOD,进一步可得到△PDA∽△POD,结合相似三角形的性质即可得到OA的长.
,结合ED的长即可得到PD的长;由圆内接四边形的对角互补可得到∠ABE+∠ADE=180°,结合平角和平行线的性质可得到∠PDA=∠AOD,进一步可得到△PDA∽△POD,结合相似三角形的性质即可得到OA的长.
(1)∵![]() ,
,![]()
∴![]()
∵![]() 是
是![]() 的直径
的直径
∴![]()
∴![]()
∴![]()
即![]()
又∵![]() 是
是![]() 的直径
的直径
∴![]() 是
是![]() 的切线
的切线
(2)∵∠DEA和∠ABD都是![]() 所对的圆周角,
所对的圆周角,
∴∠DEA=∠ABD
∵BD平分∠ABE
∴∠ABD=∠DBE
∴∠DEA=∠DBE
∵∠EDB=∠BDE,∠DEA=∠DBE,
∴△DEF∽△DBE,
∴![]()
∴![]()
(3)根据题意画出图形,连接DA、DO
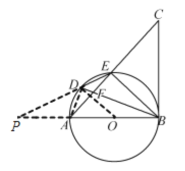
∵OD=OB,
∴∠ODB=∠OBD
∵∠EBD=∠OBD
∴∠EBD=∠ODB
∴OD∥BE
∴![]()
∵PA=AO
∴PA=AO=OB,
∴![]()
∴![]()
∴![]()
∵DE=2,
∴PD=4
∵∠PDA+∠ADE=180°,∠ABE+∠ADE=180°,
∴∠PDA=∠ABE
∵OD∥BE
∴∠AOD=∠ABE,
∴∠PDA=∠AOD
∵∠P=∠P,∠PDA=∠AOD
∴△PDA∽△POD
∴![]()
设OA=x,则PA=x,PO=2x
∵PD=4,![]() ,PA=x,PO=2x
,PA=x,PO=2x
∴![]()
∴x=![]()
∴OA=![]()
故答案为:![]()

 单元期中期末卷系列答案
单元期中期末卷系列答案【题目】某同学在利用描点法画二次函数y=ax2+bx+c(a=0)的图象时,先取自变量x的一些值,计算出相应的函数值y,如下表所示:
x | … | 0 | 1 | 2 | 3 | 4 | … |
y | … | ﹣3 | 0 | ﹣1 | 0 | 3 | … |
接着,他在描点时发现,表格中有一组数据计算错误,他计算错误的一组数据是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()