题目内容
1.按要求解下列方程组(1)用代入法解方程组$\left\{\begin{array}{l}{3x-y=7(1)}\\{5x+2y=8(2)}\end{array}\right.$
(2)用加减法解方程组$\left\{\begin{array}{l}{8x+5y=9(1)}\\{3x-5y=13(2)}\end{array}\right.$.
分析 (1)方程组利用代入消元法求出解即可;
(2)方程组利用加减消元法求出解即可.
解答 解:(1)由(1)得:y=3x-7,
代入(2)得:5x+2(3x-7)=8,
去括号得:5x+6x-14=8,即11x=22,
解得:x=2,
把x=2代入得:y=-1,
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$;
(2)(1)+(2)得:11x=22,即x=2,
把x=2代入(1)得:y=1.4,
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=1.4}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
相关题目
12.在下列各数中,最小的数是( )
| A. | 1 | B. | -1 | C. | -3 | D. | 0 |
16.点P位于y轴右侧,距y轴3个单位长度;位于x轴下方,距x轴4个单位长度,点P的坐标为( )
| A. | (-3,4) | B. | (3,-4) | C. | (-4,3) | D. | (4,-3) |
11.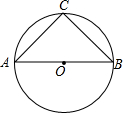 若等腰直角三角形的外接圆半径的长为2,则等腰直角三角形的直角边长为( )
若等腰直角三角形的外接圆半径的长为2,则等腰直角三角形的直角边长为( )
 若等腰直角三角形的外接圆半径的长为2,则等腰直角三角形的直角边长为( )
若等腰直角三角形的外接圆半径的长为2,则等腰直角三角形的直角边长为( )| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{2}$-2 | C. | 2-$\sqrt{2}$ | D. | $\sqrt{2}$-1 |
 已知在△ABC中,∠BAC=90°,AD⊥BC于点D,点E为AC中点,延长ED、AB交于点F.求证:$\frac{AB}{AC}$=$\frac{DF}{FA}$.
已知在△ABC中,∠BAC=90°,AD⊥BC于点D,点E为AC中点,延长ED、AB交于点F.求证:$\frac{AB}{AC}$=$\frac{DF}{FA}$. 如图数表是由从1 开始的连续自然数组成.下面所给的判断中,正确的有①②③.(填序号)
如图数表是由从1 开始的连续自然数组成.下面所给的判断中,正确的有①②③.(填序号)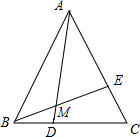 已知:如图,△ABC是等边三角形,点D、E分别在BC,AC且BD=CE,AD、BE相交于点M.求证:
已知:如图,△ABC是等边三角形,点D、E分别在BC,AC且BD=CE,AD、BE相交于点M.求证: