题目内容
14.已知点A的坐标为(2x+y-3,x-2y),它关于x轴对称的点A′的坐标为(x+3,y-4),则点A关于y轴对称的点的坐标为(-8,3).分析 由A的坐标为(2x+y-3,x-2y),它关于x轴对称的点A′的坐标为(x+3,y-4),得到方程组$\left\{\begin{array}{l}{2x+y-3=x+3}\\{x-2y+y-4=0}\end{array}\right.$,求得A(8,3),于是得到点A关于y轴对称的点的坐标为(-8,3).
解答 解:∵A的坐标为(2x+y-3,x-2y),它关于x轴对称的点A′的坐标为(x+3,y-4),
∴$\left\{\begin{array}{l}{2x+y-3=x+3}\\{x-2y+y-4=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=5}\\{y=1}\end{array}\right.$,
∴A(8,3),
∴点A关于y轴对称的点的坐标为(-8,3),
故答案为:(-8,3).
点评 此题主要考查了关于x、y轴对称点的坐标,关键是掌握点的坐标的变化规律.

练习册系列答案
相关题目
5.若|a|=3,|b|=4,且|a-b|=b-a,则ab等于( )
| A. | 12 | B. | -12 | C. | 12或-12 | D. | 不能确定 |
 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足是D,试问∠ACD和∠A的大小有什么关系?∠BCD和∠A呢?
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足是D,试问∠ACD和∠A的大小有什么关系?∠BCD和∠A呢?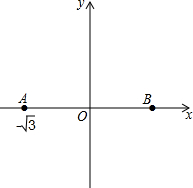 如图,在平面直角坐标系中,点A的坐标为(-$\sqrt{3}$,0),点A关于原点的对称点为B
如图,在平面直角坐标系中,点A的坐标为(-$\sqrt{3}$,0),点A关于原点的对称点为B