题目内容

8．若关于x的一元二次方程ax2+bx+c=0（a≠0）的两根分别是-3和1，则抛物线y=ax2+bx+c（a≠0）的对称轴为x=-1．

分析 已知一元二次方程ax2+bx+c=0（a≠0）的两根分别是-3和1，所以抛物线与x轴交点的横坐标为-3和1，所以对称轴为x=$\frac{-3+1}{2}$=-1．

解答 解：∵ax2+bx+c=0的两根分别是-3和1，
∴抛物线y=ax2+bx+c与x轴交点的横坐标为-3和1，
∴对称轴为x=$\frac{-3+1}{2}$=-1．

点评 本题考查抛物线与x轴的交点与对称轴的关系，若抛物线与x轴交点的坐标为x1和x2，则抛物线的对称轴为x=$\frac{{x}_{1}+{x}_{2}}{2}$

练习册系列答案
相关题目
18．若方程组$\left\{\begin{array}{l}{\frac{1}{2}x＜1}\\{x＞a}\end{array}\right.$有2个整数解，则a的取值范围为（　　）
A．-1＜a＜0B．-1≤a＜0C．-1＜a≤0D．-1≤a≤0
19．平面直角坐标系中，点A的坐标为（4，5），把OA绕点O逆时针旋转90°，那么A点旋转后所到点的横坐标是-5．
16．计算：
（1）-$\sqrt{（\sqrt{2}-\sqrt{3}）^{2}}$-2|$\sqrt{2}$-$\sqrt{3}$|-|-$\sqrt{3}$|；
（2）$\root{3}{（-1）^{2}}$+$\root{3}{-8}$-|1-$\sqrt{3}$|；
（3）$\root{3}{\frac{1}{8}}$-$\frac{5}{2}$$\root{3}{-\frac{1}{125}}$+$\root{3}{-343}$-$\root{3}{27}$．
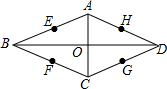3．如图，菱形ABCD的对角线AC、BD相交于点O，E、F、G、H分别是AB、BC、CD、DA的中点，点E、F、G、H在以点O为圆心的同一个圆上吗？为什么？
13．在实数-$\frac{2}{3}$，0，$\sqrt{3}$，π，0.$\stackrel{•}{5}$$\stackrel{•}{2}$中，无理数有2个．
20．已知抛物线y=$\frac{1}{2}$x2+2x-k．
（1）与x轴总有一个交点，求k的取值范围；
（2）若抛物线与x轴的两个交点的横坐标为x1、x2，且满足x12+x22=k2-k+6，求抛物线的解析式．
10．下列计算正确的是（　　）
A．a2+a2=2a4B．（-a2b）3=-a6b3C．a2•a4=a4D．a4÷a2=a4
11．已知，点A、B在数轴上对应的数分别为2和-3，则线段AB的长度为5．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网