题目内容
20. 如图,⊙O是等边三角形ABC的外接圆,⊙O的半径为3,则等边三角形ABC的边长为( )
如图,⊙O是等边三角形ABC的外接圆,⊙O的半径为3,则等边三角形ABC的边长为( )| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | 3$\sqrt{3}$ | D. | 3$\sqrt{2}$ |
分析 首先连接OB,OC,过点O作OD⊥BC于D,由⊙O是等边△ABC的外接圆,即可求得∠OBC的度数,然后由三角函数的性质即可求得OD的长,又由垂径定理即可求得等边△ABC的边长.
解答 解:连接OB,OC,过点O作OD⊥BC于D,
∴BC=2BD,
∵⊙O是等边△ABC的外接圆,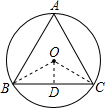
∴∠BOC=$\frac{1}{3}$×360°=120°,
∵OB=OC,
∴∠OBC=∠OCB=$\frac{180°-∠BOC}{2}$=$\frac{180°-120°}{2}$=30°,
∵⊙O的半径为3,
∴OB=3,
∴BD=OB•cos∠OBD=2×cos30°=3×$\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{2}$,
∴BC=2BD=3$\sqrt{3}$,
∴等边△ABC的边长为3$\sqrt{3}$,
故选C.
点评 本题主要考查了垂径定理,圆的内接等边三角形,以及三角函数的性质等知识.此题难度不大,解题的关键是掌握数形结合思想的应用与辅助线的作法.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
11.下列说法正确的是( )
| A. | 锐角和钝角一定互补 | B. | 一个角的补角一定大于这个角 | ||
| C. | 两点可以确定无数条直线 | D. | 钝角的补角一定是锐角 |
12.某服装店原计划按每套200元的价格销售一批保暖内衣,但上市后销售不佳,为减少库存积压,两次连续降价打折处理,最后价格调整为每套128元.若两次降价折扣率相同,则每次降价率为( )
| A. | 8% | B. | 18% | C. | 20% | D. | 25% |
9.平面直角坐标系内点P(m,2),与Q(-1,n)关于原点对称,则下列结果正确的是( )
| A. | m=1,n=-2 | B. | m=-1,n=2 | C. | m=-1,n=-2 | D. | m=1,n=2 |
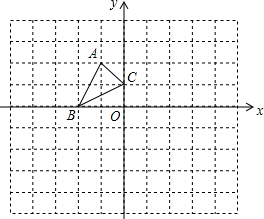 △ABC平面在直角坐标系中的位置如图所示(其中每个小正方形的边长均为1),点A(-1,2),点B(-2,0),点C(0,1).
△ABC平面在直角坐标系中的位置如图所示(其中每个小正方形的边长均为1),点A(-1,2),点B(-2,0),点C(0,1).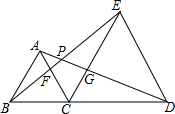 如图,△ABC和△ECD都是等边三角形,连接BE和AD,AC交BE于点F,AD交CE于点G,AD交BE于点P.
如图,△ABC和△ECD都是等边三角形,连接BE和AD,AC交BE于点F,AD交CE于点G,AD交BE于点P.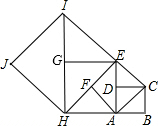 如图,如果以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去…,已知正方形ABCD的面积S1为1,按上述方法所作的正方形的面积依次为S2,S3,…,Sn(n为正整数),那么第2015个正方形的面积S2015为22014.
如图,如果以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去…,已知正方形ABCD的面积S1为1,按上述方法所作的正方形的面积依次为S2,S3,…,Sn(n为正整数),那么第2015个正方形的面积S2015为22014.