题目内容
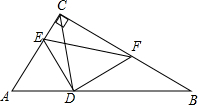 如图,在Rt△ABC中,∠BCA=90°,∠A=60°,CD是角平分线,在CB上截取CF=CA.
如图,在Rt△ABC中,∠BCA=90°,∠A=60°,CD是角平分线,在CB上截取CF=CA.(1)求证:DF=BF;
(2)若AE=BF,求∠CFE的度数.
考点:全等三角形的判定与性质
专题:
分析:(1)证明△ACD≌△FCD,得∠CDF=∠ADC=75°,AD=DF,再结合条件可求得∠BDF=30°=∠B可得出结论;
(2)结合(1)可证得△ADE为等边三角形,再结合条件可证明△EDF为等腰直角三角形,可求得∠CFE.
(2)结合(1)可证得△ADE为等边三角形,再结合条件可证明△EDF为等腰直角三角形,可求得∠CFE.
解答:(1)证明:
∵∠A=60°,∠ACD=45°,
∴∠ADC=75°,
在△ACD和△FCD中
∴△ACD≌△FCD(SAS),
∴∠CDF=∠ADC=75°,AD=DF,
∴∠BDF=30°=∠B,
∴DF=BF;
(2)解:
∵AE=BF=DF=AD,∠A=60°,
∴△ADE为等边三角形,
∴∠ADE=60°,
∴∠EDF=180°-60°-30°=90°,∠CDE=75°-60°=15°,
∵ED=AD=DF,
∴△EDF为等腰直角三角形,
∴∠DEF=∠FCD=45°,
∴∠CFE=∠CDE=15°.
∵∠A=60°,∠ACD=45°,
∴∠ADC=75°,
在△ACD和△FCD中
|
∴△ACD≌△FCD(SAS),
∴∠CDF=∠ADC=75°,AD=DF,
∴∠BDF=30°=∠B,
∴DF=BF;
(2)解:
∵AE=BF=DF=AD,∠A=60°,
∴△ADE为等边三角形,
∴∠ADE=60°,
∴∠EDF=180°-60°-30°=90°,∠CDE=75°-60°=15°,
∵ED=AD=DF,
∴△EDF为等腰直角三角形,
∴∠DEF=∠FCD=45°,
∴∠CFE=∠CDE=15°.
点评:本题主要考查全等三角形的判定和性质,充分利用条件找到可能全等的三角形是解题的关键.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
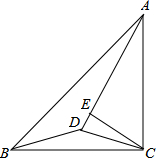 已知AC=BC,∠ACB=90°,∠DCB=15°,BD=CD,CE⊥AD于点E,求证:BC=2CE.
已知AC=BC,∠ACB=90°,∠DCB=15°,BD=CD,CE⊥AD于点E,求证:BC=2CE. 如图,在△ABC中,AB=AC,D是BC的中点,E是BA延长线上一点,F是AC上一点,且AE=AF,连接EF并延长交BC于点G,证明:AD∥EG.
如图,在△ABC中,AB=AC,D是BC的中点,E是BA延长线上一点,F是AC上一点,且AE=AF,连接EF并延长交BC于点G,证明:AD∥EG.