题目内容
已知圆的半径为5,一弦长为8,则该弦中点到弦所对应的弧的中点的距离为 .
考点:垂径定理,勾股定理
专题:
分析:过圆心O作垂直于弦的直径,构造直角三角形,利用垂径定理及勾股定理即可解决问题.
解答: 解:在⊙O中,弦AB=8,半径R=5;
解:在⊙O中,弦AB=8,半径R=5;
过圆心O作直径MN,且MN⊥AB于点C,连接OB;
则AC=BC=
AB=4,OB=5,
由勾股定理得:OC=
=
=3,
则CM=5+3=8,CN=5-3=2;
∵MN⊥AB,且MN为⊙O的直径,
∴点M、N分别为
、
的中点,
∴AB弦中点到弦所对应的弧的中点的距离分别为2或8.
 解:在⊙O中,弦AB=8,半径R=5;
解:在⊙O中,弦AB=8,半径R=5;过圆心O作直径MN,且MN⊥AB于点C,连接OB;
则AC=BC=
| 1 |
| 2 |
由勾股定理得:OC=
| 52-42 |
| 9 |
则CM=5+3=8,CN=5-3=2;
∵MN⊥AB,且MN为⊙O的直径,
∴点M、N分别为
 |
| AMB |
 |
| ANB |
∴AB弦中点到弦所对应的弧的中点的距离分别为2或8.
点评:该题考查了垂径定理及其推论的应用问题;解题的关键是作垂直于弦的直径,构造直角三角形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
整式x2-y2与x2+y2的和是( )
| A、2x2 |
| B、2y2 |
| C、-2x2 |
| D、-2y2 |
下列判断正确的是( )
| A、0.380精确到0.01 |
| B、5.6万精确到0.1 |
| C、300精确到个位 |
| D、1.60×104精确到百分位 |
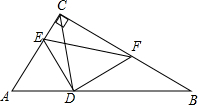 如图,在Rt△ABC中,∠BCA=90°,∠A=60°,CD是角平分线,在CB上截取CF=CA.
如图,在Rt△ABC中,∠BCA=90°,∠A=60°,CD是角平分线,在CB上截取CF=CA. 如图,已知等边△ABC中,AE=CD且AF=
如图,已知等边△ABC中,AE=CD且AF= 如图,延长线段AB到C,使BC=2AB,若AC=6cm,且AD=DB,BE:EF:FC=1:1:3,求DE、DF的长.
如图,延长线段AB到C,使BC=2AB,若AC=6cm,且AD=DB,BE:EF:FC=1:1:3,求DE、DF的长. 已知菱形ABCD,F为AC上一点,AF=5,∠ABF=90°,边CD上有一点E,CE=1,∠CFE=45°,求菱形ABCD的边长.
已知菱形ABCD,F为AC上一点,AF=5,∠ABF=90°,边CD上有一点E,CE=1,∠CFE=45°,求菱形ABCD的边长.