题目内容
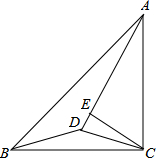 已知AC=BC,∠ACB=90°,∠DCB=15°,BD=CD,CE⊥AD于点E,求证:BC=2CE.
已知AC=BC,∠ACB=90°,∠DCB=15°,BD=CD,CE⊥AD于点E,求证:BC=2CE.考点:角平分线的性质,全等三角形的判定与性质,等腰直角三角形
专题:证明题
分析:以DC为边在△ACD内作等边三角形DCM,先证得△ACM≌△BCD得出∠MAC=∠DBC=15°,进而得出∠AMD=∠AMC,从而证得△ACM≌△ADM,证得∠MAD=∠MAC=15°,得出∠CAD=2∠MAC=30°,根据含30°的直角三角形的性质得出AC=2CE,即可得出BC=2CE.
解答: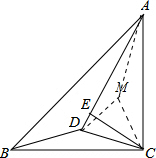 证明:以DC为边在△ACD内作等边三角形DCM
证明:以DC为边在△ACD内作等边三角形DCM
∴∠DCM=∠CMD=∠CDM=60°;CD=DM=CM
又BD=CD;∠DCB=15°
∴∠CBD=∠DCB=15°
∵AC=BC;∠ACB=90°
∴∠ACM=90°-∠BCD-∠DCM=15°=∠BCD,
在△ACM和△BCD中,
,
∴△ACM≌△BCD(SAS)
∴∠MAC=∠DBC=15°
∴∠AMC=180°-∠ACM-∠CAM=150°
∴∠AMD=360°-∠AMC-∠CMD=150°=∠AMC,
在△ACM和△ADM中,
,
∴△ACM≌△ADM(SAS),
∴∠MAD=∠MAC=15°,
∴∠CAD=2∠MAC=30°,
又CE⊥AE,
∴AC=2CE,
∴BC=2CE.
 证明:以DC为边在△ACD内作等边三角形DCM
证明:以DC为边在△ACD内作等边三角形DCM∴∠DCM=∠CMD=∠CDM=60°;CD=DM=CM
又BD=CD;∠DCB=15°
∴∠CBD=∠DCB=15°
∵AC=BC;∠ACB=90°
∴∠ACM=90°-∠BCD-∠DCM=15°=∠BCD,
在△ACM和△BCD中,
|
∴△ACM≌△BCD(SAS)
∴∠MAC=∠DBC=15°
∴∠AMC=180°-∠ACM-∠CAM=150°
∴∠AMD=360°-∠AMC-∠CMD=150°=∠AMC,
在△ACM和△ADM中,
|
∴△ACM≌△ADM(SAS),
∴∠MAD=∠MAC=15°,
∴∠CAD=2∠MAC=30°,
又CE⊥AE,
∴AC=2CE,
∴BC=2CE.
点评:本题考查了等边三角形的性质,等腰直角三角形的性质,三角形全等的判定和性质,含30°的直角三角形的性质等,熟练掌握性质是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列计算正确的是( )
| A、-1+1=0 | ||
| B、-2-2=0 | ||
C、4÷
| ||
| D、-|-5|=5 |
下列判断正确的是( )
| A、0.380精确到0.01 |
| B、5.6万精确到0.1 |
| C、300精确到个位 |
| D、1.60×104精确到百分位 |
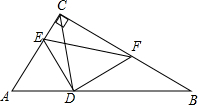 如图,在Rt△ABC中,∠BCA=90°,∠A=60°,CD是角平分线,在CB上截取CF=CA.
如图,在Rt△ABC中,∠BCA=90°,∠A=60°,CD是角平分线,在CB上截取CF=CA. 如图,延长线段AB到C,使BC=2AB,若AC=6cm,且AD=DB,BE:EF:FC=1:1:3,求DE、DF的长.
如图,延长线段AB到C,使BC=2AB,若AC=6cm,且AD=DB,BE:EF:FC=1:1:3,求DE、DF的长.