题目内容
14.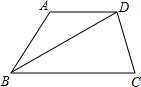 如图,在梯形ABCD中,AD∥BC,AD=AB,BC=BD,∠A=140°,则∠C等于( )
如图,在梯形ABCD中,AD∥BC,AD=AB,BC=BD,∠A=140°,则∠C等于( )| A. | 75° | B. | 60° | C. | 70° | D. | 80° |
分析 先由等腰三角形的性质和三角形内角和定理求出∠ADB,再由平行线得出同旁内角互补,即可求出∠C.
解答 解:∵AD=AB,BC=BD,∠A=140°,
∴∠ABD=∠ADB=$\frac{1}{2}$(180°-140°)=20°,∠BDC=∠C,
∵AD∥BC,
∴∠ADC+∠C=180°,
即∠ADB+∠BDC+∠C=180°,
∴2∠C=160°,
∴∠C=80°,
故选:D.
点评 本题考查了梯形的性质、等腰三角形的性质、平行线的性质;根据题意弄清各个角之间的数量关系是解决问题的关键.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
6.下列函数中,一定是二次函数的是( )
| A. | $y=-\sqrt{2}{x^2}$ | B. | y=ax2+bx+c | C. | $y=\frac{1}{x^2}$ | D. | y=(k2+1)x |
3.下列各式中,一定能成立的是( )
| A. | $\sqrt{{{({-2.5})}^2}}={({\sqrt{2.5}})^2}$ | B. | $\sqrt{a^2}=a$ | C. | $\sqrt{{x^2}-2x+1}=x-1$ | D. | $\sqrt{{x^2}-9}=\sqrt{x-3}•\sqrt{x+3}$ |
4.已知x,y是有理数,则代数式x2y2+x2+y2-4xy+2的值一定是( )
| A. | 非负数 | B. | 正数 | C. | 不小于1 | D. | 不小于2 |
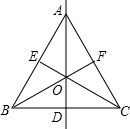 如图是一个轴对称图形,AD所在的直线是对称轴,仔细观察图形,回答下列问题:
如图是一个轴对称图形,AD所在的直线是对称轴,仔细观察图形,回答下列问题: