题目内容
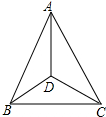如图，在△ABC中，AD平分∠BAC，且BD=CD，求证：∠B=∠C．考点：等腰三角形的判定与性质
专题：证明题
分析：根据角平分线的性质定理求得DE=DF，然后根据HL证得RT△BDE≌RT△CDF，得出∠ABD=∠ACD，根据等边对等角得出∠DBC=∠DCB，进而证得∠B=∠C．
解答：
解：过点D作DE⊥AB于E，作DF⊥AC于F，
∵AD平分∠BAC，
∴DE=DF，
在RT△BDE与RT△CDF中，
，
∴RT△BDE≌RT△CDF（HL），
∴∠ABD=∠ACD，
∵BD=CD，
∴∠DBC=∠DCB，
∴∠ABD+∠DBC=∠ACD+∠DCB，
即∠B=∠C．
解：过点D作DE⊥AB于E，作DF⊥AC于F，∵AD平分∠BAC，
∴DE=DF，
在RT△BDE与RT△CDF中，
|
∴RT△BDE≌RT△CDF（HL），
∴∠ABD=∠ACD，
∵BD=CD，
∴∠DBC=∠DCB，
∴∠ABD+∠DBC=∠ACD+∠DCB，
即∠B=∠C．
点评：本题考查了角平分线的性质，三角形全等的判定和性质，等腰三角形的性质，熟练掌握性质和定理是解题的关键．
练习册系列答案
赢在课堂名师课时计划系列答案
相关题目
已知，抛物线y=-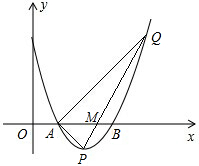
如图，二次函数图象的顶点是P（2，-1），与x轴交于点A和点B（3，0）
在图中，∠DAC和∠ABC都为直角．BC长为3，AB长为4，AD长为12，求以DC为边的正方形的面积．