题目内容
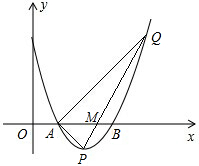 如图,二次函数图象的顶点是P(2,-1),与x轴交于点A和点B(3,0)
如图,二次函数图象的顶点是P(2,-1),与x轴交于点A和点B(3,0)(1)求这个二次函数的解析式;
(2)点Q为第一象项的抛物线上一点,且AQ⊥PA.
①求S△PAQ的值;
②PQ交x轴于M,求
| MP |
| MQ |
考点:二次函数综合题
专题:压轴题
分析:(1)设二次函数顶点式解析式y=a(x-2)2-1(a≠0),然后把点B的坐标代入求出a的值,即可得解;
(2)①令y=0求出点A的坐标,然后求出∠PAB=45°,再求出∠BAQ=45°,然后求出直线AQ的解析式,再与二次函数解析式联立求出点Q的坐标,再利用勾股定理列式求出AP、AQ的长,然后利用三角形的面积公式列式计算即可得解;
②根据等底的三角形的面积的比等于高的比求出S△APM:S△AMQ,再根据等高的三角形的面积的比等于底边的比求解即可.
(2)①令y=0求出点A的坐标,然后求出∠PAB=45°,再求出∠BAQ=45°,然后求出直线AQ的解析式,再与二次函数解析式联立求出点Q的坐标,再利用勾股定理列式求出AP、AQ的长,然后利用三角形的面积公式列式计算即可得解;
②根据等底的三角形的面积的比等于高的比求出S△APM:S△AMQ,再根据等高的三角形的面积的比等于底边的比求解即可.
解答:解:(1)设二次函数顶点式解析式y=a(x-2)2-1(a≠0),
将点B(3,0)代入得,a(3-2)2-1=0,
解得a=1,
所以,函数解析式为y=(x-2)2-1=x2-4x+3,
即y=x2-4x+3;
(2)①令y=0,则x2-4x+3=0,
解得x1=1,x2=3,
所以,点A的坐标为(1,0),
∵顶点P(2,-1),
∴∠PAB=45°,
∵AQ⊥PA,
∴∠BAQ=90°-45°=45°,
∴直线AQ的解析式为y=x-1,
联立
,
解得
,
,
∴点Q的坐标为(4,3),
由勾股定理得,AP=
=
,
AQ=
=3
,
∴S△PAQ=
×
×3
=3;
②∵点P(2,-1),Q(4,3),
∴S△APM:S△AMQ=1:3,
∵点A到PQ的距离相等,
∴
=
=
.
将点B(3,0)代入得,a(3-2)2-1=0,
解得a=1,
所以,函数解析式为y=(x-2)2-1=x2-4x+3,
即y=x2-4x+3;
(2)①令y=0,则x2-4x+3=0,
解得x1=1,x2=3,
所以,点A的坐标为(1,0),
∵顶点P(2,-1),
∴∠PAB=45°,
∵AQ⊥PA,
∴∠BAQ=90°-45°=45°,
∴直线AQ的解析式为y=x-1,
联立
|
解得
|
|
∴点Q的坐标为(4,3),
由勾股定理得,AP=
| (2-1)2+(-1-0)2 |
| 2 |
AQ=
| (4-1)2+(3-0)2 |
| 2 |
∴S△PAQ=
| 1 |
| 2 |
| 2 |
| 2 |
②∵点P(2,-1),Q(4,3),
∴S△APM:S△AMQ=1:3,
∵点A到PQ的距离相等,
∴
| MP |
| MQ |
| S△APM |
| S△AMQ |
| 1 |
| 3 |
点评:本题是二次函数综合题型,主要利用了待定系数法求二次函数解析式,联立两函数解析式求交点坐标,两点间的距离的求解,等底的三角形的面积的比等于高的比,等高的三角形的面积的比等于底边的比.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
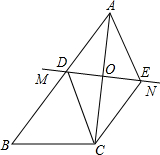 如图,△ABC中,AC的垂直平分线MN交AB于点D,交AC于点O,CE∥AB交MN于E,连结AE、CD.
如图,△ABC中,AC的垂直平分线MN交AB于点D,交AC于点O,CE∥AB交MN于E,连结AE、CD.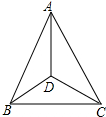 如图,在△ABC中,AD平分∠BAC,且BD=CD,求证:∠B=∠C.
如图,在△ABC中,AD平分∠BAC,且BD=CD,求证:∠B=∠C. 如图,已知线段AB=10cm,AP=6cm,P是OB的中点,则A0=
如图,已知线段AB=10cm,AP=6cm,P是OB的中点,则A0= 如图,△ABD≌△ACE,AB=8cm,AD=3cm,则BE=
如图,△ABD≌△ACE,AB=8cm,AD=3cm,则BE=