题目内容
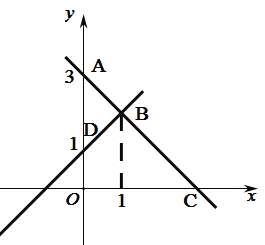
【题目】定义:如图1,在平面直角坐标系中,点M是二次函数![]() 图象上一点,过点M作
图象上一点,过点M作![]() 轴,如果二次函数
轴,如果二次函数![]() 的图象与
的图象与![]() 关于l成轴对称,则称
关于l成轴对称,则称![]() 是
是![]() 关于点M的伴随函数
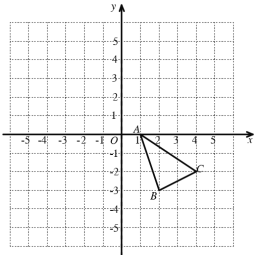
关于点M的伴随函数![]() 如图2,在平面直角坐标系中,二次函数
如图2,在平面直角坐标系中,二次函数![]() 的函数表达式是
的函数表达式是![]() ,点M是二次函数
,点M是二次函数![]() 图象上一点,且点M的横坐标为m,二次函数
图象上一点,且点M的横坐标为m,二次函数![]() 是
是![]() 关于点M的伴随函数.
关于点M的伴随函数.



![]() 若
若![]() ,
,
![]() 求
求![]() 的函数表达式.
的函数表达式.
![]() 点
点![]() ,
,![]() 在二次函数
在二次函数![]() 的图象上,若
的图象上,若![]() ,a的取值范围为______.
,a的取值范围为______.
![]() 过点M作
过点M作![]() 轴,
轴,
![]() 如果
如果![]() ,线段MN与
,线段MN与![]() 的图象交于点P,且MP:
的图象交于点P,且MP:![]() :3,求m的值.
:3,求m的值.
![]() 如图3,二次函数
如图3,二次函数![]() 的图象在MN上方的部分记为
的图象在MN上方的部分记为![]() ,剩余的部分沿MN翻折得到
,剩余的部分沿MN翻折得到![]() ,由
,由![]() 和
和![]() 所组成的图象记为
所组成的图象记为![]() .以
.以![]() 、
、![]() 为顶点在x轴上方作正方形
为顶点在x轴上方作正方形![]() 直接写出正方形ABCD与G有三个公共点时m的取值范围.
直接写出正方形ABCD与G有三个公共点时m的取值范围.
【答案】![]()
![]() 的函数表达式为
的函数表达式为![]() ,
, ![]()
![]() ;
;
![]() 或
或![]() ,
, ![]() 当
当![]() 或
或![]() 时,G与正方形ABCD有三个公共点.
时,G与正方形ABCD有三个公共点.
【解析】
![]() 根据题意,当
根据题意,当![]() 时,可得到抛物线
时,可得到抛物线![]() 的顶点为
的顶点为![]() ,再用顶点式写出函数表达式即可;
,再用顶点式写出函数表达式即可;
![]() 由点
由点![]() ,
,![]() 在二次函数
在二次函数![]() 的图象上,得到
的图象上,得到![]() ,再根据
,再根据![]() ,可得a的取值范围;
,可得a的取值范围;
![]() 由
由![]() 轴,MP:
轴,MP:![]() :3,得到
:3,得到![]() ,然后根据当m>0和m<0时,分情况讨论即可得到答案;
,然后根据当m>0和m<0时,分情况讨论即可得到答案;
![]() 通过分别分析当m=
通过分别分析当m=![]() ,1,
,1,![]() ,2值,得到正方形与G的公共点数,从而得到正方形与G有三个公共点时m的取值范围.
,2值,得到正方形与G的公共点数,从而得到正方形与G有三个公共点时m的取值范围.
![]() 当
当![]() 时,抛物线
时,抛物线![]() 与抛物线
与抛物线![]() 关于直线
关于直线![]() 对称,
对称,
![]() 抛物线
抛物线![]() 的顶点是
的顶点是![]() ,
,
![]() 抛物线
抛物线![]() 的解析式为
的解析式为![]() ;
;
![]() 点
点![]() ,
,![]() 在二次函数
在二次函数![]() 的图象上,
的图象上,
∴![]() ,
,
当![]() 时,
时,![]() ,
,
解得:![]() ,
,
故答案为:![]() ;
;
![]() 轴,MP:
轴,MP:![]() :3,
:3,
∴![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,
故![]() 或
或![]() ;
;
![]() 分析图象可知:
分析图象可知:
当![]() 时,可知C1和G的对称轴关于直线
时,可知C1和G的对称轴关于直线![]() 对称,
对称,![]() 的顶点恰在AD上,此时G与正方形有2个公共点,
的顶点恰在AD上,此时G与正方形有2个公共点,
当![]() 时,G与正方形ABCD有三个公共点,
时,G与正方形ABCD有三个公共点,
当![]() 时,直线MN与x轴重合,G与正方形有三个公共点,
时,直线MN与x轴重合,G与正方形有三个公共点,
当1<m<![]() 时,G与正方形ABCD有五个公共点,
时,G与正方形ABCD有五个公共点,
当m=![]() 时,G的顶点与点C(3,2)重合,且G对称轴左侧部分与正方形有三个公共点,
时,G的顶点与点C(3,2)重合,且G对称轴左侧部分与正方形有三个公共点,
当![]() <m<2时,G与正方形ABCD有四个个公共点,
<m<2时,G与正方形ABCD有四个个公共点,
当![]() 时,G过点
时,G过点![]() 且G对称轴左侧部分与正方形有两个公共点,
且G对称轴左侧部分与正方形有两个公共点,
故当![]() 或
或![]() 时,G与正方形ABCD有三个公共点.
时,G与正方形ABCD有三个公共点.