题目内容
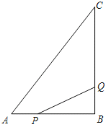
【题目】如图,正方形![]() 中,
中,![]() 是对角线
是对角线![]() 上一点,过
上一点,过![]() 点作矩形
点作矩形![]() ,其中点
,其中点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上.
上.

![]() 求
求![]() 的度数;
的度数;
![]() 试说明
试说明![]() ,
,![]() ;
;
![]() 若正方形的面积为
若正方形的面积为![]() ,求矩形
,求矩形![]() 的周长.
的周长.
【答案】(1)45°;(2)见解析; (3) 10cm.
【解析】
(1)直接根据正方形的性质即可得出结论;(2)根据四边形ABCD是正方形可知,EG∥BC,EF∥CD,所以∠DEG=45°,∠BFE=∠DGE=90°,故△DEG与△EBF是等腰直角三角形,故EG=DG,EF=BF;(3)先根据正方形的面积为25cm2求出边长,由(1)知EG=DG,EF=BF,所以EG+CG=DC,由此可得出结论.
解:![]() ∵四边形
∵四边形![]() 是正方形,
是正方形,![]() 为对角线,
为对角线,
∴![]() ;
;![]() ∵四边形
∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,
∵四边形![]() 是矩形,
是矩形,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() 与
与![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,![]() ;
;![]() ∵正方形的面积为
∵正方形的面积为![]() ,
,
∴![]() ,
,
∵由![]() 知
知![]() ,
,![]() ,
,
∴![]() ,
,
∴矩形![]() 的周长
的周长![]() .
.

练习册系列答案
相关题目