题目内容
用换元法解方程:x+ =2.
=2.
解:由
可设 ,则y-
,则y-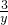 =2,整理得
=2,整理得
y2-2y-3=0,
解得y1=3,y2=-1.
当y=3时,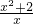 =3,x2-3x+2=0,解得x1=2,x2=1.
=3,x2-3x+2=0,解得x1=2,x2=1.
当y=-1时,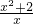 =-1,x2+x+2=0,△=1-8=-7<0,此方程没有实数根.
=-1,x2+x+2=0,△=1-8=-7<0,此方程没有实数根.
经检验:x1=2,x2=1是原方程的根.
∴原方程的根是x1=2,x2=1.
分析:本题考查用换元法解分式方程的能力.因为x+ =
=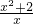 ,且
,且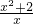 与
与 互为倒数,所以可采用换元法解分式方程.
互为倒数,所以可采用换元法解分式方程.
点评:用换元法解分式方程,可简化计算过程,减少计算量,是一种常用的方法.

可设
 ,则y-
,则y-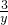 =2,整理得
=2,整理得y2-2y-3=0,
解得y1=3,y2=-1.
当y=3时,
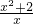 =3,x2-3x+2=0,解得x1=2,x2=1.
=3,x2-3x+2=0,解得x1=2,x2=1.当y=-1时,
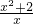 =-1,x2+x+2=0,△=1-8=-7<0,此方程没有实数根.
=-1,x2+x+2=0,△=1-8=-7<0,此方程没有实数根.经检验:x1=2,x2=1是原方程的根.
∴原方程的根是x1=2,x2=1.
分析:本题考查用换元法解分式方程的能力.因为x+
 =
=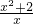 ,且
,且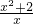 与
与 互为倒数,所以可采用换元法解分式方程.
互为倒数,所以可采用换元法解分式方程.点评:用换元法解分式方程,可简化计算过程,减少计算量,是一种常用的方法.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
用换元法解方程(x+
)2-(x+
)=2,若设a=x+
,则方程可化为( )
| 3 |
| x |
| 3 |
| x |
| 3 |
| x |
| A、a2+a+2=0 |
| B、a2-a+2=0 |
| C、a2-a-2=0 |
| D、a2+a-2=0 |
用换元法解方程(x-
)2-3x+
+2=0时,如果设x-
=y,那么原方程可转化( )
| 1 |
| x |
| 3 |
| x |
| 1 |
| x |
| A、y2+3y+2=0 |
| B、y2-3y-2=0 |
| C、y2+3y-2=0 |
| D、y2-3y+2=0 |