Question

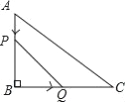
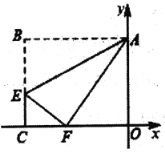
【题目】如图，在平面直角坐标系中，长方形的边，分别在轴，轴上，点在边上，将该长方形沿折叠，点恰好落在边上的点处，若，，则所在直线的表达式为__________．

Answer 1

【答案】

【解析】

设CE=a，根据勾股定理可以得到CE、OF的长度，再根据点E在第二象限，从而可以得到点E的坐标．然后利用待定系数法求出AE所在直线的解析式．

解：设CE=a，则BE=8-a，

由折叠的性质可得：EF=BE=8-a，AB=AF
∵∠ECF=90°，CF=4，
∴a2+42=（8-a）2，
解得，a=3，
∴OE=3

设OF=b，则OC=AB=AF=4+b
∵∠ACF=90°，OA=8，

∴b2+82=（b+4）2，

∴b=6，∴OF=6

∴OC=CF+OF=10，
∴点E的坐标为（-10，3），

设AE所在直线的解析式为y=kx+b（k≠0）．

将E（-10，3），A（0，8）代入y=kx+b

得，解得

∴AE所在直线的解析式为：

故答案为：