Question

【题目】如图，是的直径，是的弦，延长到点，使，连结，过点作，垂足为，交的延长线于点．

求证：为的切线；

猜想线段、、之间的数量关系，并证明你的猜想；

若，，求线段的长．

Answer 1

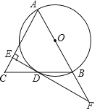
【答案】（1）证明见解析；（2）．理由见解析；（3）．

【解析】

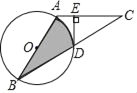
（1）连接OD，由AO=BO，BD=DC，可判断OD为△BAC的中位线，则OD∥AC，由于EF⊥AC，则EF⊥OD，于是可根据切线的判定定理得到EF为⊙O的切线；

（2）连结AD，根据圆周角定理得∠ADB=90°，而BD=CD，根据等腰三角形的判定得AB=AC，再根据等角的余角相等得到∠DAB=∠BDF，则可判断△FBD∽△FDA，得到DF：AF=BF：DF，理由比例性质得DF2=BFFA=BF（BF+AB），所以DF2=BF2+BFAC；

（3）先得到OD=，AB=AC=5．在Rt△ACD中，由正切的定义得到AD=2CD，再根据勾股定理可解得CD=．在Rt△ECD中，同样可求得CE=1，则DE=2，AE=AC﹣CE=4，然后根据△FOD∽△FAE，利用相似比可求出EF的长．

（1）连接OD，如图，∵AO=BO，BD=DC，∴OD∥AC．

∵EF⊥AC，∴EF⊥OD．

∵OD为半径，∴EF为⊙O的切线；

（2）DF2=BF2+BFAC．理由如下：

连结AD，如图，∵AB为⊙O的直径，∴∠ADB=90°，而BD=CD，∴AB=AC，∠DAB+∠ABD=90°．

∵OD⊥DF，∴∠ODB+∠BDF=90°，而OD=OB，∴∠ODB=∠OBD，∴∠DAB=∠BDF，而∠BFD=∠DFA，∴△FBD∽△FDA，∴DF：AF=BF：DF，∴DF2=BFFA，∴DF2=BF（BF+AB）

∴DF2=BF2+BFAC；

（3）∵AO=，∴OD=，AB=AC=5．在Rt△ACD中，tanC==2，∴AD=2CD．

∵AD2+CD2=AC2，∴4CD2+CD2=52，解得：CD=Rt△ECD中，tanC==2，∴DE=2CE．

∵DE2+CE2=CD2，∴4CE2+CE2=5，解得：CE=1，∴DE=2，AE=AC﹣CE=4．

∵OD∥AE，∴△FOD∽△FAE，∴=，即=，∴EF=．