题目内容
11.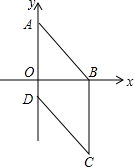 如图,在平面直角坐标系中,四边形ABCD是菱形,已知A(0,4),B(3,0).
如图,在平面直角坐标系中,四边形ABCD是菱形,已知A(0,4),B(3,0).(1)求D点的坐标;
(2)求经过C点的反比例函数的解析式.
分析 (1)由A(0,4),B(3,0),可利用勾股定理,求得AB的长,然后由四边形ABCD是菱形,可求得AD的长,则可求得OD的长,继而求得D点的坐标;
(2)由四边形ABCD是菱形,可求得点C的坐标,继而求得经过C点的反比例函数的解析式.
解答 解:(1)∵A(0,4),B(3,0),
∴OA=4,OB=3,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=5,
∵四边形ABCD是菱形,
∴AD=AB=5,
∴OD=AD-OA=1,
∴D点的坐标为:(0,-1);
(2)∵四边形ABCD是菱形,
∴AD∥BC,BC=AB=5,
∴点C的坐标为:(3,-5),
设经过C点的反比例函数的解析式为:y=$\frac{k}{x}$,
∴-5=$\frac{k}{3}$,
解得:k=-15,
∴经过C点的反比例函数的解析式为:y=-$\frac{15}{x}$.
点评 此题考查了菱形的性质以及待定系数法求反比例函数的解析式.注意掌握菱形的性质是关键.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
20.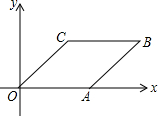 菱形OABC在平面直角坐标系中的位置如图所示,∠AOC=45°,点A的坐标为($\sqrt{2}$,0),则点B的坐标为( )
菱形OABC在平面直角坐标系中的位置如图所示,∠AOC=45°,点A的坐标为($\sqrt{2}$,0),则点B的坐标为( )
 菱形OABC在平面直角坐标系中的位置如图所示,∠AOC=45°,点A的坐标为($\sqrt{2}$,0),则点B的坐标为( )
菱形OABC在平面直角坐标系中的位置如图所示,∠AOC=45°,点A的坐标为($\sqrt{2}$,0),则点B的坐标为( )| A. | ($\sqrt{2}$,1) | B. | (1,$\sqrt{2}$) | C. | (1,$\sqrt{2}$+1) | D. | ($\sqrt{2}$+1,1) |
1.钓鱼岛自古以来就是中国的固有领土,在“百度”搜索引擎中输入“钓鱼岛最新消息”,能搜索到与之相关的结果个数约为4640000,这个数字用科学记数法表示为( )
| A. | 464×104 | B. | 46.4×106 | C. | 4.64×106 | D. | 0.464×107 |