题目内容
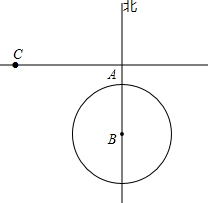 如图,一轮船以40km/h的速度由西向东航行,在途中点C处接到台风警报,台风中心点B正以20km/h的速度由南向北移动.已知距台风中心200km的区域(包括边界)都属于受台风影响区.当轮船接到台风警报时,测得BC=500km,BA=300km.(假定轮船不改变航向).
如图,一轮船以40km/h的速度由西向东航行,在途中点C处接到台风警报,台风中心点B正以20km/h的速度由南向北移动.已知距台风中心200km的区域(包括边界)都属于受台风影响区.当轮船接到台风警报时,测得BC=500km,BA=300km.(假定轮船不改变航向).(1)轮船会不会受到台风影响?并说明理由;
(2)如果轮船受到台风影响,请求出台影响的时间;
(3)如果轮船受到台风影响,请求出台风影响最强烈的时刻.
考点:勾股定理的应用
专题:
分析:(1)先根据勾股定理求出AC的长,再设当轮船接到报警后经过t小时受到台风影响,根据勾股定理列出关于t的方程求出t的值即可;
(2)根据(1)中t的值即可得出结论;
(3)求出t的中间值即可.
(2)根据(1)中t的值即可得出结论;
(3)求出t的中间值即可.
解答: 解:(1)轮船会受到台风影响.
解:(1)轮船会受到台风影响.
∵BC=500km,BA=300km,
∴AC=
=400km.
设当轮船接到报警后经过t小时受到台风影响,则
(400-30t)2+(300-20t)2=2002,
解得t1≈8.35,t2≈19.34,
∴轮船会受到台风影响;
(2)∵由(1)知,从8.35小时到19.34小时轮船受到台风影响,
∴台影响的时间=19.34-8.35=10.99(小时).
答:台影响的时间是10.99小时.
(3))∵由(1)知,从8.35小时到19.34小时轮船受到台风影响,
∴台风影响最强烈的时刻=
+8.34=13.835(小时).
答:再经过13.835小时,轮船受台风影响最强烈.
 解:(1)轮船会受到台风影响.
解:(1)轮船会受到台风影响.∵BC=500km,BA=300km,
∴AC=
| 5002-3002 |
设当轮船接到报警后经过t小时受到台风影响,则
(400-30t)2+(300-20t)2=2002,
解得t1≈8.35,t2≈19.34,
∴轮船会受到台风影响;
(2)∵由(1)知,从8.35小时到19.34小时轮船受到台风影响,
∴台影响的时间=19.34-8.35=10.99(小时).
答:台影响的时间是10.99小时.
(3))∵由(1)知,从8.35小时到19.34小时轮船受到台风影响,
∴台风影响最强烈的时刻=
| 10.99 |
| 2 |
答:再经过13.835小时,轮船受台风影响最强烈.
点评:本题考查的是勾股定理的应用,在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.

练习册系列答案
相关题目
 如图,“日”字形窗厨的木条总长是7cm,若窗框的宽是xcm,那么窗框的高是
如图,“日”字形窗厨的木条总长是7cm,若窗框的宽是xcm,那么窗框的高是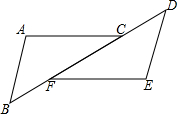 如图∠A=∠E,AB∥DE,BF=CD,说明AC与EF的关系.
如图∠A=∠E,AB∥DE,BF=CD,说明AC与EF的关系.