题目内容
20.观察下列有规律的一列数:$\frac{1}{2}$,$\frac{1}{6}$,$\frac{1}{12}$,$\frac{1}{20}$,$\frac{1}{30}$,$\frac{1}{42}$…根据规律可知$\frac{1}{2}$=$\frac{1}{1}$×$\frac{1}{2}$=$\frac{1}{1}$-$\frac{1}{2}$,$\frac{1}{6}$=$\frac{1}{2}$×$\frac{1}{3}$=$\frac{1}{2}$-$\frac{1}{3}$…
(1)$\frac{1}{110}$是第10个数;
(2)计算:$\frac{1}{2}$+$\frac{1}{6}$+$\frac{1}{12}$+$\frac{1}{20}$+…+$\frac{1}{110}$.
(3)计算:$\frac{1}{2}$+$\frac{1}{2×4}$+$\frac{1}{4×6}$+$\frac{1}{6×8}$+$\frac{1}{8×10}$+…+$\frac{1}{18×20}$.
分析 (1)分母都是可以拆成两个连续自然数的乘积,第一个因数就是这个数所在的位置,因为110=10×11,所以$\frac{1}{110}$是第10个数;
(2)利用规律把分数拆分计算即可;
(3)提取$\frac{1}{4}$,进一步拆分得出答案即可.
解答 解:(1)$\frac{1}{110}$是第10个数;
(2)$\frac{1}{2}$+$\frac{1}{6}$+$\frac{1}{12}$+$\frac{1}{20}$+…+$\frac{1}{110}$
=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{5}$+…+$\frac{1}{10}$-$\frac{1}{11}$
=1-$\frac{1}{11}$
=$\frac{10}{11}$.
(3)$\frac{1}{2}$+$\frac{1}{2×4}$+$\frac{1}{4×6}$+$\frac{1}{6×8}$+$\frac{1}{8×10}$+…+$\frac{1}{18×20}$
=$\frac{1}{4}$×(2+1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{5}$+…+$\frac{1}{9}$-$\frac{1}{10}$)
=$\frac{1}{4}$×(3-$\frac{1}{10}$)
=$\frac{1}{4}$×$\frac{29}{10}$
=$\frac{29}{40}$.
点评 此题考查有理数的混合运算,掌握数据的规律,正确拆分得出答案即可.

 阅读快车系列答案
阅读快车系列答案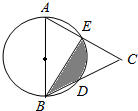 如图,AB是⊙O的直径,点D、E是半圆的三等分点,AE、BD的延长线交于点C.若CE=3,则图中由线段BD,BE和弧DE围成的阴影部分的面积是( )
如图,AB是⊙O的直径,点D、E是半圆的三等分点,AE、BD的延长线交于点C.若CE=3,则图中由线段BD,BE和弧DE围成的阴影部分的面积是( )| A. | $\frac{4}{3}$π-$\sqrt{3}$ | B. | $\frac{3}{2}π$ | C. | $\frac{2}{3}$π-$\sqrt{3}$ | D. | $\frac{8}{3}π$ |
①数轴上的点只能表示整数;
②数轴上的点只能表示有理数;
③数轴是一条直线;
④数轴上找不到既不表示正数,又不表示负数的点;
⑤所有理数都可以数轴上的点表示出来;
⑥数轴上的一个点只能表示一个数.
其中正确的有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
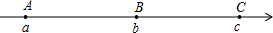 如图,数轴上的A、B、C三点所表示的数分别是a、b、c,其中AB=BC,如果|a|<|b|<|c|,那么该数轴的原点O的位置应该在( )
如图,数轴上的A、B、C三点所表示的数分别是a、b、c,其中AB=BC,如果|a|<|b|<|c|,那么该数轴的原点O的位置应该在( )| A. | 点A与点B之间靠近A点 | B. | 点A与点B之间靠近A点或点A的左边 | ||
| C. | 点B与点C之间靠近C点 | D. | 点B与点C之间靠近C点或点C的右边 |
 如图是10×10的网格中,每个方格的边长均为1,刘亮在该网格中标出A,B两点的相对位置,已知点A的位置用(6,2)表示,点B的位置用(9,5)表示.
如图是10×10的网格中,每个方格的边长均为1,刘亮在该网格中标出A,B两点的相对位置,已知点A的位置用(6,2)表示,点B的位置用(9,5)表示. 如图,△OCA≌△OBD,则这两个三角形中相等的边有AC=BD,OC=OB,OA=OD,相等的角有∠A=∠D,∠C=∠B,∠AOC=∠DOB.
如图,△OCA≌△OBD,则这两个三角形中相等的边有AC=BD,OC=OB,OA=OD,相等的角有∠A=∠D,∠C=∠B,∠AOC=∠DOB. 如图,直线l1∥l2,∠2=120°,则∠1=60度.
如图,直线l1∥l2,∠2=120°,则∠1=60度. 如图,已知?ABCD中,DE⊥AC,BF⊥AC,证明:四边形DEBF为平行四边形.
如图,已知?ABCD中,DE⊥AC,BF⊥AC,证明:四边形DEBF为平行四边形.