题目内容
下列各点在抛物线y=-x2+1上的是( )
| A、(1,0) |
| B、(0,0) |
| C、(0,-1) |
| D、(1,1) |
考点:二次函数图象上点的坐标特征
专题:计算题
分析:分别计算自变量为1和0时的函数值,然后根据二次函数图象上点的坐标特征进行判断.
解答:解:∵当x=1时,y=-x2+1=0;当x=0,y=-x2+1=1,
∴点(1,0)在抛物线y=-x2+1上.
故选A.
∴点(1,0)在抛物线y=-x2+1上.
故选A.
点评:本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.

练习册系列答案
相关题目
已知线段AB=4,点P是它的黄金分割点,AP>PB,则PB=( )
A、
| ||||
B、
| ||||
C、2
| ||||
D、6-2
|
若一个正方形的边长为4,则它的面积是( )
| A、8 | B、12 | C、16 | D、20 |
 如图,已知∠1=∠2,欲证△ABD≌△ACD,还必须从下列选项中补选一个,则错误的选项是( )
如图,已知∠1=∠2,欲证△ABD≌△ACD,还必须从下列选项中补选一个,则错误的选项是( )| A、∠ADB=∠ADC |
| B、∠B=∠C |
| C、BD=CD |
| D、AB=AC |
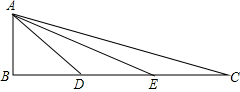 如图,在△ABC中,∠B=90°,点D、E在BC上,且AB=BD=EC=DE,求证:
如图,在△ABC中,∠B=90°,点D、E在BC上,且AB=BD=EC=DE,求证: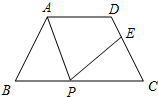 如图,在等腰梯形ABCD中,AD∥BC,AD=3,BC=7,∠B=60°,P为BC边上一点(不与B、C重合).过点P作∠APE=∠B,PE交CD于E.
如图,在等腰梯形ABCD中,AD∥BC,AD=3,BC=7,∠B=60°,P为BC边上一点(不与B、C重合).过点P作∠APE=∠B,PE交CD于E. 如图示,PA,PB分别与⊙O相切于点A,B,⊙O的切线EF分别交PA,PB于点E,F,切点C在弧AB上,若PA=12,则△PEF的周长是?
如图示,PA,PB分别与⊙O相切于点A,B,⊙O的切线EF分别交PA,PB于点E,F,切点C在弧AB上,若PA=12,则△PEF的周长是?