题目内容
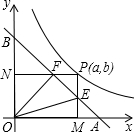 如图,已知直角坐标系内有一条直线和一条曲线,这条直线和x轴、y轴正半轴分别交于点A和点B,且OA=OB=1.这条曲线是函数y=
如图,已知直角坐标系内有一条直线和一条曲线,这条直线和x轴、y轴正半轴分别交于点A和点B,且OA=OB=1.这条曲线是函数y=| 1 |
| 2x |
| 3 |
| 4 |
| 2 |
| 3 |
(1)分别求出点E、F的坐标;
(2)求△OEF的面积;
(3)分别计算AF与BE的值;
(4)△AOF与△BOE是否一定相似,请予以证明;如果不一定相似或一定不相似,简要说明理由.
考点:反比例函数综合题
专题:代数几何综合题,探究型,数形结合
分析:(1)首先求得直线AB的解析式,E的横坐标是
,代入解析式即可求得纵坐标,F的纵坐标是
,代入解析式即可求得横坐标;
(2)利用割补法求得S△EOF=S矩形MONP-S△EMO-S△FNO-S△EPF;
(3)根据相似三角形的判定定理SAS证明△AOF∽△BOE.
| 3 |
| 4 |
| 2 |
| 3 |
(2)利用割补法求得S△EOF=S矩形MONP-S△EMO-S△FNO-S△EPF;
(3)根据相似三角形的判定定理SAS证明△AOF∽△BOE.
解答:(1)解:设直线AB的解析式是y=kx+b,
根据题意,得:
,
解得:
,
则直线AB的解析式是:y=-x+1,
当x=
时,y=
;
当y=
时,x=
.
则点E(
,
),点F(
,
);
(2)解:S△EOF=S矩形MONP-S△EMO-S△FNO-S△EPF
=
-
×
×
-
×
×
-
×(
+
-1)2
=
-
-
-
=
;
(3)解:BE=
=
,
AF=
=
;
(4)△AOF∽△BEO,
证明:∵OA=OB=1,
∴∠FAO=∠EBO;
∵AF•BE=1;
又∵OA•OB=1,
∴
=
;
∴△AOF∽△BEO.
根据题意,得:
|
解得:
|
则直线AB的解析式是:y=-x+1,
当x=
| 3 |
| 4 |
| 1 |
| 4 |
当y=
| 2 |
| 3 |
| 1 |
| 3 |
则点E(
| 3 |
| 4 |
| 1 |
| 4 |
| 1 |
| 3 |
| 2 |
| 3 |
(2)解:S△EOF=S矩形MONP-S△EMO-S△FNO-S△EPF
=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 4 |
| 2 |
| 3 |
=
| 1 |
| 2 |
| 3 |
| 32 |
| 1 |
| 9 |
| 25 |
| 288 |
=
| 5 |
| 24 |
(3)解:BE=
(
|
3
| ||
| 4 |
AF=
(
|
2
| ||
| 3 |
(4)△AOF∽△BEO,
证明:∵OA=OB=1,
∴∠FAO=∠EBO;
∵AF•BE=1;
又∵OA•OB=1,
∴
| AF |
| OB |
| OA |
| BE |
∴△AOF∽△BEO.
点评:本题主要考查了反比例函数的综合题、相似三角形的判定及勾股定理.解答(4)题时,利用反比例函数图象上的点的特点,图象上所有的点都满足函数解析式.

练习册系列答案
相关题目
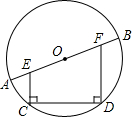 如图,在⊙O中,CD为弦,EC⊥CD,FD⊥CD,EC,FD分别交直径AB于E,F两点.
如图,在⊙O中,CD为弦,EC⊥CD,FD⊥CD,EC,FD分别交直径AB于E,F两点. 作图题:
作图题: