题目内容
2.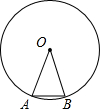 如图,AB为⊙O的内接正多边形的一边,已知∠OAB=70°,则这个正多边形的内角和为1260°.
如图,AB为⊙O的内接正多边形的一边,已知∠OAB=70°,则这个正多边形的内角和为1260°.
分析 由圆的性质易证△OAB是等腰三角形,所以∠AOB的度数可求,再根据正多边形的性质可求出其边数,最后利用多边形内角和定理计算即可.
解答 解:
∵OA=OB,
∴∠OAB=∠OBA=70°,
∴∠AOB=40°,
∵AB为⊙O的内接正多边形的一边,
∴正多边形的边数=$\frac{360}{40}$=9,
∴这个正多边形的内角和=(9-2)×180°=1260°,
故答案为:1260°.
点评 本题考查了正多边形和圆的有关知识、等腰三角形的判断和性质以及多边形内角和定理的运用,熟记多边形内角和定理计算公式是解题的关键.

练习册系列答案
相关题目
13.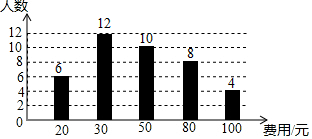 某校开展“阅读季”活动,小明调查了班级里40名同学计划购书的花费情况,并将结果绘制成如图所示的条形统计图,根据图中相关信息,这次调查获取的样本数据的众数和中位数分别是( )
某校开展“阅读季”活动,小明调查了班级里40名同学计划购书的花费情况,并将结果绘制成如图所示的条形统计图,根据图中相关信息,这次调查获取的样本数据的众数和中位数分别是( )
 某校开展“阅读季”活动,小明调查了班级里40名同学计划购书的花费情况,并将结果绘制成如图所示的条形统计图,根据图中相关信息,这次调查获取的样本数据的众数和中位数分别是( )
某校开展“阅读季”活动,小明调查了班级里40名同学计划购书的花费情况,并将结果绘制成如图所示的条形统计图,根据图中相关信息,这次调查获取的样本数据的众数和中位数分别是( )| A. | 12和10 | B. | 30和50 | C. | 10和12 | D. | 50和30. |
10. 如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,这个规律是( )
如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,这个规律是( )
 如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,这个规律是( )
如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,这个规律是( )| A. | ∠A=∠1+∠2 | B. | 2∠A=∠1+∠2 | C. | 3∠A=2∠1+∠2 | D. | 3∠A=2(∠1+∠2) |
17.已知2,2,x,4,9,这组数据的平均数是4,则这组数据的中位数和众数分别是( )
| A. | 2和2 | B. | 4和2 | C. | 2和3 | D. | 3和2 |