Question

14．在△ABC中，∠ABC=90°，D为△ABC内一动点，BD=a，CD=b（其中a，b为常数，且a＜b）．将△CDB沿CB翻折，得到△CEB．连接AE．
（1）请在图（1）中补全图形；
（2）若∠ACB=α，AE⊥CE，则∠AEB=α；
（3）在（2）的条件下，用含a，b，α的式子表示AE的长．

Answer 1

分析 （1）根据条件画出图象即可．
（2）结论：∠AEB=α．先证明△EOC∽△OBA，得$\frac{EO}{OB}$=$\frac{CO}{OA}$，推出$\frac{EO}{OC}$=$\frac{OB}{OA}$，再证明△EOB∽△COA即可解决问题．
（3）如图2中，过点B作BF⊥BE，交AE于点F，先证明△EBC∽△FBA，分别求出EF，AF即可解决问题．

解答 解：（1）图象如图1所示，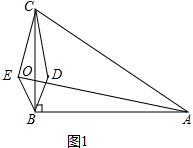


（2）结论：∠AEB=α．
理由：如图1中，设BC与AE交于点O，
∵AE⊥EC，
∴∠CEO=∠OBA，
∵∠EOC=∠BOA，
∴△EOC∽△OBA，
∴$\frac{EO}{OB}$=$\frac{CO}{OA}$，
∴$\frac{EO}{OC}$=$\frac{OB}{OA}$，∵∠EOB=∠COD，
∴△EOB∽△COA，
∴∠OEB=∠ACO=α．
故答案为α．

（3）如图2中，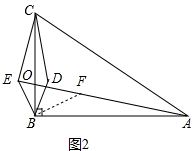

∵AE⊥CE
∴∠AEC=90°，
∵∠AEB=α，
∴∠BEC=90°+α，
过点B作BF⊥BE，交AE于点F，
则有∠FBE=90°．
即∠EBC+∠CBF=90°．
∵∠ABC=∠FBA+∠CBF=90°，
∴∠EBC=∠FBA．
∵∠BFA=∠AEB+∠EBF=90°+α．
∴∠BEC=∠BFA
∴△EBC∽△FBA．
∴$\frac{BA}{BC}=\frac{BF}{BE}=\frac{FA}{EC}$=tanα．
∵BD=a，CD=b，
∴BE=a，EC=b．
∴EF=$\frac{a}{cosα}$，AF=b•tanα．
∴AE=EF+AF=$\frac{a}{cosα}$+b•tanα．

点评 本题参考三角形综合题、相似三角形的判定和性质等知识，解题的关键是正确寻找相似三角形，利用相似三角形性质解决问题，属于中考常考题型．