题目内容

2．如图所示，小丽用棋子摆成三角形的图案，观察下面图案并填空：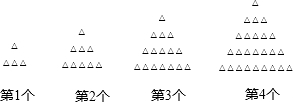

按照这样的方式摆下去，摆第5个三角形图案需要36枚棋子；摆第n个三角形图案需要（n+1）2枚棋子（用含有n的代数式表示）；摆第100个三角形图案需要10201枚棋子．

分析 从第1个三角形图案所摆的棋子数开始计算，发现规律：是连续奇数的和，结果是（n+1）2，从而依次得出结论．

解答 解：第1个三角形图案：1+3=4=22，
第2个三角形图案：1+3+5=9=32，
第3个三角形图案：1+3+5+7=16=42，
第4个三角形图案：1+3+5+7+9=16+9=25=52，
第5个三角形图案：1+3+5+7+9+11=25+11=36，
则第n个三角形图案：1+3+5+7+9+11+…+2n-1=（n+1）2，
第100个三角形图案：1012=（100+1）2=10000+200+1=10201，
故答案为：36，（n+1）2，10201．

点评 本题是图形与数字类的变化规律的综合问题，首先要探寻规律，认真观察、仔细思考，善用联想来解决这类问题；本题不仅要从图形中看规律，还要从数字变化看规律，两方面结合得出结论．

练习册系列答案
相关题目
12．-32+（-$\frac{1}{5}$）×（-15）÷（-3）×（-1）100．
13．化简求值：2a2b2+（2b2-a2）-（a2+2b2），其中a=$\frac{1}{3}$，b=3．
10．如果2$\overrightarrow{a}$+$\overrightarrow{b}$=3$\overrightarrow{c}$，$\overrightarrow{a}$+2$\overrightarrow{b}$=$\overrightarrow{0}$，那么$\overrightarrow{a}$、$\overrightarrow{b}$是平行向量吗？求$\frac{|\overrightarrow{a}|}{|\overrightarrow{b}|}$．
17．已知抛物线L1经过A（0，3），B（3，0），C（4，3），将抛物线L1向上平移得到抛物线L2，使L2的顶点恰好落在x轴上
（1）求抛物线L2的解析式及对称轴；
（2）求两抛物线和它们的对称轴及y轴所围成的阴影部分的面积．
7．已知等腰三角形的一腰长为20cm，底边长为30cm，求底角的正弦值．
14．如图是某月的日历
（1）带阴影的方框中的9个数之和与方框正中心的数有什么关系？
（2）不改变方框的大小如果将带阴影的方框移至其他几个位置试一试，你能得出什么结论？你知道为什么吗？
（3）这个结论对于任何一个月的日历都成立吗？
14．人字架、起重机的底座，输电线路支架等，在日常生活中，很多物体都采用三角形结构，这是利用了三角形的稳定性．
15．如图，在平面直角坐标系xOy中，A（0，4），P（t，0）是x轴正半轴上的一个动点，M是线段AP的中点，将线段MP绕点P顺时针旋转90°得线段PB，过B作x轴的垂线、过点A作y轴的垂线，两直线相交于点D，在P点运动过程中，当t=2时，点D落在双曲线y=$\frac{16}{x}$上．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网