题目内容
17. 已知抛物线L1经过A(0,3),B(3,0),C(4,3),将抛物线L1向上平移得到抛物线L2,使L2的顶点恰好落在x轴上
已知抛物线L1经过A(0,3),B(3,0),C(4,3),将抛物线L1向上平移得到抛物线L2,使L2的顶点恰好落在x轴上(1)求抛物线L2的解析式及对称轴;
(2)求两抛物线和它们的对称轴及y轴所围成的阴影部分的面积.
分析 (1)把点A、B、C代入抛物线解析式y=ax2+bx+c利用待定系数法求解即可;
(2)把抛物线解析式整理成顶点式形式,然后写出顶点坐标与对称轴,然后根据顶点坐标求出向上平移的距离,再根据阴影部分的面积等于平行四边形的面积,列式进行计算即可得解.
解答 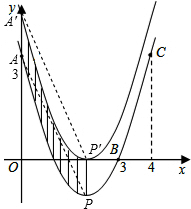 解:(1)∵抛物线y=ax2+bx+c经过点A(0,3),B(3,0),C(4,3),
解:(1)∵抛物线y=ax2+bx+c经过点A(0,3),B(3,0),C(4,3),
∴$\left\{\begin{array}{l}{c=3}\\{9a+3b+c=0}\\{16a+4b+c=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=1}\\{b=-4}\\{c=3}\end{array}\right.$,
所以抛物线的函数表达式为y=x2-4x+3;
(2)∵y=x2-4x+3=(x-2)2-1,
∴抛物线的顶点坐标为(2,-1),对称轴为直线x=2;
∴PP′=1,
阴影部分的面积等于平行四边形A′APP′的面积,
平行四边形A′APP′的面积=1×2=2,
∴阴影部分的面积=2.
点评 本题考查了待定系数法求二次函数解析式,二次函数的性质,二次函数图象与几何变换,(3)根据平移的性质,把阴影部分的面积转化为平行四边形的面积是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.若关于x的方程kx2-(k+1)x+1=0的根是整数,则满足条件的整数k的个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |