题目内容
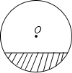
【题目】一根水平放置的圆柱形输水管道的横截面如图所示，其中有水部分水面宽
米，最深处水深
米，则此输水管道的直径等于（ ）
A. 
米 B. 
米 C. 米 D. 
米
【答案】D
【解析】
过O作OE⊥AB交AB于点D，连接OA、OB，由垂径定理可知AD=
AB，再设OA=r，则OD=r-DE=r-0.1，再在Rt△OAD中利用勾股定理即可求出R的值，进而求出输水管道的直径．
过O作OE⊥AB交AB于点D，连接OA、OB，
则AD=AB=×0.4=0.2米，
设OA=r，则OD=r-DE=r-0.1，
在Rt△OAD中，
OA2=AD2+OD2，即r2=0.22+（r-0.1）2，解得r=0.25米，
故此输水管道的直径=2r=2×0.25=0.5米．
故选D．
练习册系列答案
相关题目
【题目】某公司根据市场计划调整投资策略，对
，
两种产品进行市场调查，收集数据如表：
项目 产品 | 年固定成本 （单位：万元） | 每件成本 （单位：万元） | 每件产品销售价 （万元） | 每年最多可生产的件数 |
|
|
|
|
|
|
|
|
|
|
其中
是待定常数，其值是由生产的材料的市场价格决定的，变化范围是
，销售产品时需缴纳
万元的关税，其中
为生产产品的件数，假定所有产品都能在当年售出，设生产，两种产品的年利润分别为
、
（万元），写出、与之间的函数关系式，注明其自变量的取值范围．