题目内容
9. 如图,在平面直角坐标系中,三角板AOB的边OB在x轴上,∠ABO=90°,∠A=30°且OB=2,将△ABO绕点B逆时针旋转到△A′BO′,当原点O在A′O′上时,点A′的坐标为(-1,$\sqrt{3}$).
如图,在平面直角坐标系中,三角板AOB的边OB在x轴上,∠ABO=90°,∠A=30°且OB=2,将△ABO绕点B逆时针旋转到△A′BO′,当原点O在A′O′上时,点A′的坐标为(-1,$\sqrt{3}$).
分析 作A'C⊥x轴,在RT△ABO中求出AO、∠AOB,根据旋转性质知△BOO'为等边三角形,进而知RT△A'OC中,A'O=2、∠A'OC=60°,根据三角函数可求得点A'坐标.
解答 解:如图,过点A'作A'C⊥x轴,垂足为点C,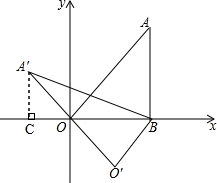
RT△ABO中,∵OB=2,∠A=30°,
∴OA=2OB=4,∠AOB=60°,
又∵由旋转性质可得:OB=O'B=2,O'A'=0A=4,∠AOB=∠A'O'B'=60°,
∴△BOO'是等边三角形,OO'=0B=O'B=2,
∴∠A'OC=∠BOO'=60°,OA'=O'A'-OO'=2,
在RT△A'OC中,A'C=OA'sin∠A'OC=2×sin60°=$\sqrt{3}$,
CO=OA'cos∠A'OC=2×cos60°=1,
则A'的坐标为(-1,$\sqrt{3}$),
故答案为:(-1,$\sqrt{3}$).
点评 本题主要考查因旋转的变化中点的坐标,熟悉旋转的性质是根本,利用旋转的性质得到有利的线段长度和角的大小是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.下列图形,是中心对称图形但不是轴对称图形的是( )
| A. | 等边三角形 | B. | 平行四边形 | C. | 圆 | D. | 正五边形 |
18.下列各式正确的是( )
| A. | -8+3=5 | B. | (-2)3=6 | C. | -(a-b)=-a+b | D. | 2(a+b)=2a+b |
19.若3x=a,3y=b,则3x-2y等于( )
| A. | $\frac{a}{{b}^{2}}$ | B. | 2ab | C. | a+$\frac{2}{b}$ | D. | $\frac{a}{2b}$ |
 如图,函数y=-3x和y=kx+b的图象相交于点A(m,4),则关于x的不等式kx+b+3x>0的解集为x>-$\frac{4}{3}$.
如图,函数y=-3x和y=kx+b的图象相交于点A(m,4),则关于x的不等式kx+b+3x>0的解集为x>-$\frac{4}{3}$. 如图,点P是∠AOB内一点.
如图,点P是∠AOB内一点.