题目内容
9.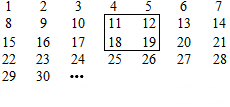 把连续的正整数1,2,3,4…按如图所示方式排列,用正方形框,按如图所示方式任意框住4个数,记框中左上角的数为x.
把连续的正整数1,2,3,4…按如图所示方式排列,用正方形框,按如图所示方式任意框住4个数,记框中左上角的数为x.(1)被框住的4个数的和是4x+16.(用含x的代数式表示)
(2)当被框住的4个数之和等于244时,x的值为多少?
(3)这样的正方形框所框住的4个数的和能等于380吗?若能,请求出x的值;若不能,请说明理由.
分析 (1)根据数的排布规律即可找出框中的四个数,将其相加即可得出结论;
(2)结合(1)以及被框住的4个数之和等于244即可得出关于x的一元一次方程,解之即可得出结论;
(3)结合(1)以及被框住的4个数之和等于380即可得出关于x的一元一次方程,解之即可求出x的值,由x的值为7的整数倍结合图形即可得出这样的正方形框住4个数的和不能等于380.
解答 解:(1)∵记框中左上角的数为x,
∴框中的四个数分别为:x、x+1、x+7、x+8,
∴被框住的4个数的和是x+x+1+x+7+x+8=4x+16.
故答案为:4x+16.
(2)根据题意得:4x+16=244,
解得:x=57.
答:当被框住的4个数之和等于244时,x的值为57.
(3)不能,理由如下:
根据题意得:4x+16=380,
解得:x=91,
∵91=7×13,
∴91是第13行的最后一个数,
∴这样的正方形框住4个数的和不能等于380.
点评 本题考查了一元一次方程的应用以及列代数式,根据正方形框住4个数的和列出一元一次方程是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.下列说法正确的是( )
| A. | 打开电视机,正在播放“安岳新闻”,是必然事件 | |
| B. | 从装有10个红球的袋子中,摸出1个白球是不可能事件 | |
| C. | 某种彩票的中奖率为1%,则买100张彩票一定有张中奖 | |
| D. | “明天降雨的概率是80%”,表示明天有80%的时间降雨 |
 如图,在△ABC中,点D、E分别在边AB、AC上,$\frac{AD}{AC}$=$\frac{AE}{AB}$,∠BAC的平分线AG分别交线段DE、BC于点F、G.
如图,在△ABC中,点D、E分别在边AB、AC上,$\frac{AD}{AC}$=$\frac{AE}{AB}$,∠BAC的平分线AG分别交线段DE、BC于点F、G. 如图,已知“人字梯”的5个踩档把梯子等分成6份,从上往下的第二个踩档与第三个踩档的正中间处有一条60cm长的绑绳EF,tanα=$\frac{5}{2}$,则“人字梯”的顶端离地面的高度AD是180cm.
如图,已知“人字梯”的5个踩档把梯子等分成6份,从上往下的第二个踩档与第三个踩档的正中间处有一条60cm长的绑绳EF,tanα=$\frac{5}{2}$,则“人字梯”的顶端离地面的高度AD是180cm.