Question

如图，将一块直角三角板OAB放在平面直角坐标系中，B（2，0），∠AOB=60°，点A在第一象限，过点A的双曲线为y=

k

x

，在x轴上取一点P，过点P作直线OA的垂线l，以直线l为对称轴，线段OB经轴对称变换后的像是O′B′．设P（t，0）当点O′落在双曲线y=

k

x

上时，则t=

 

．

Answer 1

考点：反比例函数综合题

专题：

分析：当点O′落在双曲线y=

k

x

上时点O′与点A重合，即点O与点A重合，进一步解直角三角形AOB，利用轴对称的现在解答即可；

解答：解：点O′落在双曲线y=

k

x

上时点O′与点A重合，直线l垂直平分OA，如图，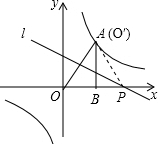
连PA，则PA=PO，
∵B（2，0），∠AOB=60°，
∴OB=2，
∴AB=

3

OB=2

3

，
∵P点坐标为（t，0），则PA=PO=t，PB=t-2，
在Rt△PAB中，PA²=PB²+AB²，即t²=（t-2）²+（2

3

）²，解得t=4，
故答案为：4．

点评：本题考查了轴对称变换的性质：轴对称变换不改变原图形的形状和大小，即变换后图形与原图形全等．也考查了勾股定理以及含30度的直角三角形三边的关系．