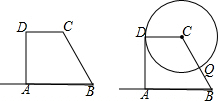题目内容
4. 小华为了测量楼房AB的高度,他从楼底的B处沿着斜坡向上行走20m,到达坡顶D处.已知斜坡的坡角为15°.小华的身高ED是1.6m,他站在坡顶看楼顶A处的仰角为45°,求楼房AB的高度.(计算结果精确到1m)
小华为了测量楼房AB的高度,他从楼底的B处沿着斜坡向上行走20m,到达坡顶D处.已知斜坡的坡角为15°.小华的身高ED是1.6m,他站在坡顶看楼顶A处的仰角为45°,求楼房AB的高度.(计算结果精确到1m)(参考数据:sin15°=$\frac{1}{4}$,cos15°=$\frac{24}{25}$,tan15°=$\frac{7}{26}$)
分析 作DH⊥AB于H,根据余弦的定义求出BC,根据正弦的定义求出CD,结合题意计算即可.
解答 解:作DH⊥AB于H,
∵∠DBC=15°,BD=20,
∴BC=BD•cos∠DBC=20×$\frac{24}{25}$=19.2,CD=BD•sin∠DBC=20×$\frac{1}{4}$=5,
由题意得,四边形ECBF和四边形CDHB是矩形,
∴EF=BC=19.2,BH=CD=5,
∵∠AEF=45°,
∴AF=EF=19.2,
∴AB=AF+FH+HB=19.2+1.6+5=25.8≈26m,
答:楼房AB的高度约为26m.
点评 本题考查的是解直角三角形的应用-仰角俯角问题和坡度坡角问题,掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键.

练习册系列答案
相关题目
14.方程组$\left\{\begin{array}{l}x-y=3\\ 2x+y=6\end{array}\right.$的解为( )
| A. | $\left\{\begin{array}{l}x=3\\ y=4\end{array}\right.$ | B. | $\left\{\begin{array}{l}x=3\\ y=0\end{array}\right.$ | C. | $\left\{\begin{array}{l}x=6\\ y=1\end{array}\right.$ | D. | $\left\{\begin{array}{l}x=6\\ y=-1\end{array}\right.$ |
15.按下面的程序计算,若开始输入的x为正数,最后输出的结果为56,则满足条件的x的不同的值有( )个.


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
12.将5280000用科学记数法表示,正确的是( )
| A. | 5.28×l07 | B. | 5.28×106 | C. | 52.8×105 | D. | 0.528×108 |
13.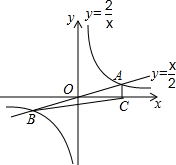 如图,正比例函数y=$\frac{x}{2}$与反比例函数y=$\frac{2}{x}$的图象交于A,B两点,AC⊥x轴于点C,连接BC,则△BOC的面积为( )
如图,正比例函数y=$\frac{x}{2}$与反比例函数y=$\frac{2}{x}$的图象交于A,B两点,AC⊥x轴于点C,连接BC,则△BOC的面积为( )
 如图,正比例函数y=$\frac{x}{2}$与反比例函数y=$\frac{2}{x}$的图象交于A,B两点,AC⊥x轴于点C,连接BC,则△BOC的面积为( )
如图,正比例函数y=$\frac{x}{2}$与反比例函数y=$\frac{2}{x}$的图象交于A,B两点,AC⊥x轴于点C,连接BC,则△BOC的面积为( )| A. | 2 | B. | $\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | 1 |
 作图题
作图题