题目内容
4.将长为a cm的线段进行黄金分割,则较长线段与较短线段之差为($\sqrt{5}$-2)acm.分析 根据黄金分割的定义得到较长线段为$\frac{\sqrt{5}-1}{2}$a,则较短线段长为a-$\frac{\sqrt{5}-1}{2}$a=$\frac{3-\sqrt{5}}{2}$a,然后计算它们的差即可.
解答 解:长为a cm的线段进行黄金分割,则较长线段为$\frac{\sqrt{5}-1}{2}$a,较短线段长为a-$\frac{\sqrt{5}-1}{2}$a=$\frac{3-\sqrt{5}}{2}$a,
它们的差为$\frac{\sqrt{5}-1}{2}$a-$\frac{3-\sqrt{5}}{2}$a=($\sqrt{5}$-2)acm.
故答案为($\sqrt{5}$-2)a.
点评 本题考查了黄金分割:把线段AB分成两条线段AC和BC(AC>BC),且使AC是AB和BC的比例中项(即AB:AC=A:BC),叫做把线段AB黄金分割,点C叫做线段AB的黄金分割点.其中AC=$\frac{\sqrt{5}-1}{2}$AB≈0.618AB,并且线段AB的黄金分割点有两个.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
19.$\sqrt{x}$+$\sqrt{y}$的一个有理化因式是( )
| A. | $\sqrt{x+y}$ | B. | $\sqrt{x}-\sqrt{y}$ | C. | $\sqrt{x}+\sqrt{y}$ | D. | $\sqrt{x-y}$ |
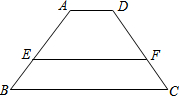 如图,梯形ABCD中,AD∥BC∥EF,AE:EB=2:3,AD=12,则BC=18,则EF=14.4.
如图,梯形ABCD中,AD∥BC∥EF,AE:EB=2:3,AD=12,则BC=18,则EF=14.4. 如图所示,是某工件的三视图,求此工件的体积.(结果保留π)
如图所示,是某工件的三视图,求此工件的体积.(结果保留π) 在数轴上分别画出点A、B、C、D,点A表示数$\frac{1}{3}$,点B表示数1$\frac{1}{2}$,点C表示数0,点D表示数2$\frac{3}{4}$;并将点A、B、C、D所表示的数用“>”连接.
在数轴上分别画出点A、B、C、D,点A表示数$\frac{1}{3}$,点B表示数1$\frac{1}{2}$,点C表示数0,点D表示数2$\frac{3}{4}$;并将点A、B、C、D所表示的数用“>”连接.