Question

16．已知直角三角形的两条直角边长分别是3厘米，4厘米，则此直角三角形的重心与外心之间的距离为$\frac{5}{6}$ 厘米．

Answer 1

分析 根据勾股定理求出斜边的长度，根据斜边中线长为斜边长的一半求出斜边的中线CD，由重心定理即可得出GD的长．

解答 解：如图所示：连接CD，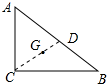
∵∠ACB=90°，
∴斜边AB=$\sqrt{{3}^{2}+{4}^{2}}$=5厘米，
∴斜边AB的中线CD=$\frac{1}{2}$×5=$\frac{5}{2}$厘米，
∵D为Rt△ABC的外心，G是重心，
∴由重心定理得：GD=$\frac{1}{3}$CD=$\frac{5}{6}$厘米．
故答案为：$\frac{5}{6}$．

点评 本题考查了勾股定理、直角三角形斜边上的中线性质、重心的性质；熟练掌握勾股定理和重心定理，熟记直角三角形的外心是斜边的中点是解题的关键．