题目内容
13.在平面直角坐标系中,A点坐标为(3,4),将线段OA绕原点O逆时针旋转90°得到线段OA′,则点A′的坐标是( )| A. | (-4,3) | B. | (-3,4) | C. | (3,-4) | D. | (4,-3) |
分析 过点A作AB⊥x轴于B,过点A′作A′B′⊥x轴于B′,根据旋转的性质可得OA=OA′,利用同角的余角相等求出∠OAB=∠A′OB′,然后利用“角角边”证明△AOB和△OA′B′全等,根据全等三角形对应边相等可得OB′=AB,A′B′=OB,然后写出点A′的坐标即可.
解答 解:如图,过点A作AB⊥x轴于B,过点A′作A′B′⊥x轴于B′,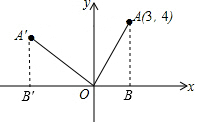
∵OA绕坐标原点O逆时针旋转90°至OA′,
∴OA=OA′,∠AOA′=90°,
∵∠A′OB′+∠AOB=90°,∠AOB+∠OAB=90°,
∴∠OAB=∠A′OB′,
在△AOB和△OA′B′中,
$\left\{\begin{array}{l}{∠OAB=∠A′OB′}\\{∠ABO=∠OB′A′}\\{OA=OA′}\end{array}\right.$,
∴△AOB≌△OA′B′(AAS),
∴OB′=AB=4,A′B′=OB=3,
∴点A′的坐标为(-4,3).
故选:A.
点评 本题考查了坐标与图形变化-旋转,熟记性质并作辅助线构造出全等三角形是解题的关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 如图,折叠长方形纸片ABCD的一边AD,使点D落在BC边上的点F处,AE为折痕.已知AB=8,BC=10,则EC的长为3.
如图,折叠长方形纸片ABCD的一边AD,使点D落在BC边上的点F处,AE为折痕.已知AB=8,BC=10,则EC的长为3.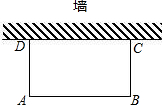 如图,某中学为中考体育加试利用一面墙(墙的长度不超过45m),用80m的铁丝网围成一个矩形体育场地.
如图,某中学为中考体育加试利用一面墙(墙的长度不超过45m),用80m的铁丝网围成一个矩形体育场地. 如图,轮船甲位于码头O的正西方向A处,轮船乙位于码头O的正北方向,测得∠CAO=45°.轮船甲自西向东匀速行驶,同时轮船乙沿正北方向匀速行驶,它们的速度分别为45km/h和36km/h,经过0.2h,轮船甲行驶至B处,轮船乙行驶至D位.测得∠DBO=58°,此时B处距离码头O有多远?
如图,轮船甲位于码头O的正西方向A处,轮船乙位于码头O的正北方向,测得∠CAO=45°.轮船甲自西向东匀速行驶,同时轮船乙沿正北方向匀速行驶,它们的速度分别为45km/h和36km/h,经过0.2h,轮船甲行驶至B处,轮船乙行驶至D位.测得∠DBO=58°,此时B处距离码头O有多远?